Лекция 10

ТЕМА 4. ВВЕДЕНИЕ В МЕХАНИКУ КОМПОЗИЦИОННЫХ

МАТЕРИАЛОВ

4.1. Задачи механики. Математическое описание сложно-напряженного состояния КМ.

Композиционные материалы на основе непрерывных волокон называется специалистами «композиты».

Основным достоинством композитов является возможность создания изделий ориентированной структуры, например, усиливая конструкцию однонаправленными волокнами в направлении действия основных нагрузок.

Это позволяет получать конструкции (стрингеры, балки, несущие элементы питательных аппаратов, мостов, ответственных изделий машиностроения и техники) в десятки раз превосходящие металлические по удельной прочности, жесткости. Однако для успешной реализации композитов сложной структуры армирования, которая соответствует действующим на изделие нагрузкам и развивающихся в нем напряжениях, необходим необычный математический аппарат.

В механике композиционных материалов используется матричное и тензорное исчисление. Однако главной задачей считается получение решения конкретной задачи через инженерные параметры 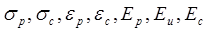, так же .

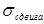В процессе эксплуатации изделий из композитов трубопроводы для перекачки нефти, сточных вод, щелочей; резервуарах для хранения и ведения технологических производств; силовых элементов изделий машиностроения, авиастроения и космической промышленности они подвергаются воздействию различных по векторам приложения, динамике, частоте, статике. Для того, чтобы рассчитывать подобные изделия и используют математический аппарат теории композиционных материалов. Рассмотрим, например, крыло летательного аппарата, которое подвергается воздействию многочисленных знакопеременных нагрузок, абсолютная величина которых составляет величину Р. Выделим в элементе изделия элементарную площадку 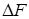, на которой локализуется действующая суммарная нагрузка. Величина Q равна пределу отношения Р на 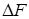при 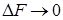, будет характеризовать вектор суммарного напряжения Q:

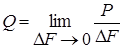
Вектор суммарного напряжения может быть разложен по трем плоскостям.

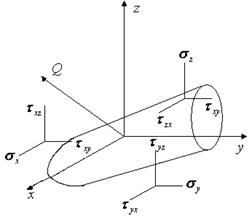
Вектор суммарного напряжения Q не имеет определенного физического смысла и не может быть воображен, поскольку он выражается 36 проекциями по трем плоскостям.