Применение уравнения Шредингера. Свободная частица

Это пробное решение. Учтем, что

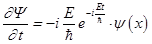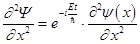и (23)

Подстановка Y(x, t) в уравнение (21)дает:

.

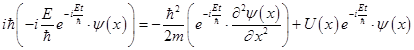После выполнения арифметических действий получаем

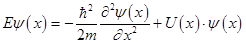. (24)

Это уравнение описывает стационарные состояния с определенным значением энергии E, поэтому его называют стационарным уравнением Шредингера.

Как выше было установлено, уравнение Шредингера для волновой функции свободной частицы массы m имеет вид (8). По заведенному порядку, выясним, что собой представляют стационарные состояния. В стационарном состоянии все амплитуды вероятности изменяются со временем синхронно с частотой E/ћ. Это значит, что волновая функция в стационарном состоянии должна зависеть от времени по закону:

Y(x, t)=y(x)×exp{–i 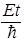}. (22)

Подстановка его в (19) дает стационарное уравнение:

Ey=– 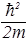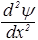. (25)

Поскольку предэкспонента y зависит только от x, постольку частная производная заменена на обыкновенную. Перепишем уравнение (25) несколько иначе:

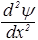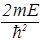+ y=0. (26)

Можно заметить, что математическое содержание уравнения (26) совпадает с содержанием уравнения движения гармонического осциллятора:

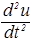+w 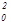y=0, (27)

где u – отклонение гармонического осциллятора от положения равновесия, w 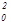– квадрат собственной частоты. Как известно, частными решениями уравнения движения гармонического осциллятора являются две экспоненты: u(t)=a×exp{±iw0t} (обычно, при описании движения классического осциллятора берут комбинацию этих двух решений, которая дает действительный косинус). В уравнении (26) роль времени играет пространственная координата, а роль квадрата собственной частоты – квадрат пространственной частоты k или волнового числа:

k²= 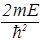. (28)

На значение энергии стационарного состояния пока не налагалось никаких условий, поэтому волновое число k – произвольная величина.

Решениями уравнения (26) являются функци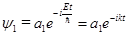и:

и 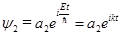. (29)

Таким образом, полные волновые функции, описывающие стационарные состояния свободной частицы, оказываются следующими:

Y1(x, t)=a×exp{i(kx– 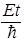)}, Y2(x, t)=a×exp{–i(kx+ 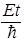)}. (30)

Функция Y1 описывает волну, бегущую в положительном направлении оси OX, а Y2 – волну, бегущую в отрицательном направлении.

Вернемся к уравнению (28). Оно дает правило определения энергии стационарного состояния:

E= 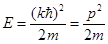. (31)

Классическая формула!

Можно сделать вывод, что стационарное состояние свободной частицы являются не только состоянием с определенным значением энергии, но и состоянием с определенным значением импульса.