Локальная теорема Лапласа.
При большом числе испытаний n вычисление Рn(k) затруднительно. В таких случаях используют приближённую формулу Лапласа.
Определение. Функция j(х) называется асимптотическим приближением функции f(х), если 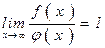 .
.
Доказано, что при 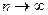 имеет место равенство:
имеет место равенство:
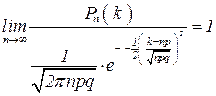 , при
, при 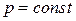 ,
, 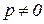 ,
, 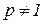 .
.
Т.е. при достаточно больших n можно пользоваться приближенной формулой:
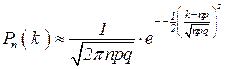 .
.
Функция 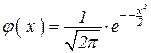 называется дифференциальной функцией Лапласа, табулирована на Х
называется дифференциальной функцией Лапласа, табулирована на Х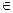 [0; 5] (см. таблица 1 приложения).
[0; 5] (см. таблица 1 приложения).
Свойства j(х):
1. j(х) определена для любых х;
2. имеет один максимум в т. А(0; 0,39);
3. имеет две точки перегиба при х = ± 1;
4. имеет одну горизонтальную асимптоту 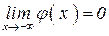 ;
; 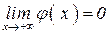 ;
;
5. 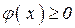 j(х) четная;;
j(х) четная;; 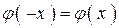 ; симметричная относительно оси ОУ;
; симметричная относительно оси ОУ;
6. при х = 5 j(х) = 0,0000015, т.е. практически при 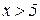
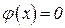 .
.
Итак, локальная формула Лапласа 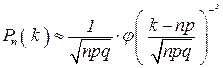 .
.
Пример Монета брошена 100 раз. Найти вероятность того, что герб появится 32 раза.
n = 100, k = 32, А: появление герба; 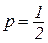 ;
; 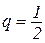 .
.
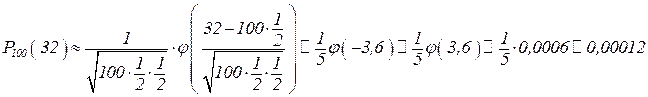
Лекция №4.
Случайные величины.
Пусть в результате опыта реализуется одно из нескольких возможных случайных событий. Если каждому исходу опыта (каждому случайному событию) поставить в соответствие некоторое число, то каждый опыт можно рассматривать как реализацию некоторой салучайной величины, в каждом опыте принимающую то или иное числовое значение. Случайная величина, таким образом - это количественная мера случайного события. Обозначать случайные величины будем символами X, Y, Z,…...
|
|
|
Определение. Случайной величиной будем называть величину, принимающую в результате опыта то или иное числовое значение, заранее до опыта неизвестное.
Различают дискретные и непрерывные случайные величины.
Определение. Случайная величина называется дискренной, если число её возможных значений конечно.
Исчерпывающей характеристикой случайной величины являются её законы распределения. Простейшей формой закона распределения дискретной случайной величины является ряд распределения – таблица, в которой перечислены все возможные значения случайной величины и указаны вероятности появления этих значений.
Пример. Пусть случайная величина Х задана рядом распределения.
| хi | ||||
| P(xi) | 0,2 | 0,4 | 0,3 | 0,1 |
Перечисленные в таблице возможные значения случайной величины составляют ПГНС, поэтому сумма вероятностей этих возможных значений всегда равна единице, т. е. 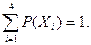
Иногда используют графическое изображение ряда распределения, его называют многоугольником распределения. На рисунке 1 изображён многоугольник распределения, соответствующий приведенному выше ряду распределения. 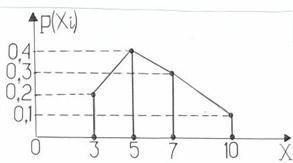
Рис.1.
Наклонные линии графика чисто условные, смысл имеют лишь ординаты, проведенные из точек оси ОХ графика.
|
|
|
Определение. Случайная величина называется непрерывной, если её увозможные значения заполняют некоторый промежуток числовой оси.
Пример. Напряжение осветительной сети переменного тока в течение суток пробегает значения, заключённеу в пределах 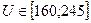 вольт
вольт
Такая форма закона распределения, как ряд распределения, для описания непрерывной случайной величины использована быть не может, так как возможных значений у такой случайной величины – бесчисленное множество. Для описания непрерывных случайных величин используют другую форму закона распределения, называемую функцией распределения или интегральным законом распределения вероятности.
Обозначают функцию распределения (в дальнейшем Ф.Р.) символом F(х).
Определение. Функцией распределения называется всякое соотношение, выражающее вероятность выполнения неравенства: F(x)=P(X<x). Здесь х – текущее значение случайной величины.
Общий вид графика функции распределения и её свойства получим из следующего эксперимента. Пусть случайная точка падает на числовую ось ОХ в любое её место. Выбираем текущее значение х* случайной величины, отмечаем её положение на числовой оси ОХ графика (см. рис. 2), и вероятность случайной точки упасть левее отмеченного значения х* обозгначим величиной F(x*). Откладываем эту вероятность по вертикальной оси графика.
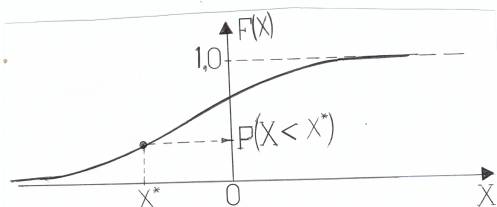
Рис.2.
Будем увеличивать аргумент х*, т. е. двигать отмеченную на рисунке 2 точку вправо по оси ОХ. При этом очевидно, что вероятность того, что случайная точка Х упадёт левее х*, не может уменьшаться, она только увеличится. Очевидно, что при 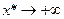 всякий опыт будет заканчиваться тем, что точка будет падать левее текущего значения х и это событие станет достоверным, вероятность его будет стремиться к единице. Если же начать точку х* двигать влево по оси ОХ, т. е. х*
всякий опыт будет заканчиваться тем, что точка будет падать левее текущего значения х и это событие станет достоверным, вероятность его будет стремиться к единице. Если же начать точку х* двигать влево по оси ОХ, т. е. х*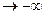 , то вероятность ожидаемого события будет уменьшаться и в пределе будет стремиться к нулю. Из приведенных рассуждений следуют свойства функции распределения F(x):
, то вероятность ожидаемого события будет уменьшаться и в пределе будет стремиться к нулю. Из приведенных рассуждений следуют свойства функции распределения F(x):
1. Функция распределения есть неубывающая функция своего аргумента, т. е. при х1>х2 имеет место F(x1)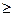 F(x2).
F(x2).
2. При х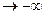 функция распределения равна нулю
функция распределения равна нулю 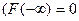 ).
).
3. При 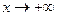 функция распределения равна единице (
функция распределения равна единице (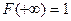 ).
).
Достоинством функции распределения является её универсальность, она
является исчерпывающей характеристикой как непрерывных, так и дискретных случайных венличин. Вид функции распределения для дискретной случайной величины, заданной своим рядом распредкеления (см. таб. выше), приведен на рис. 3. В отличии от функции распределения непрерывной случайной величины, график которой – всегда непрерывная кривая (см. рис. 2), график функции распределения дискретной случайной величины имеет «ступенчатый» характер, каждая «ступенька» соответствует своему возможному её значению, а её «высота» равна вероятности появления зтого значения.
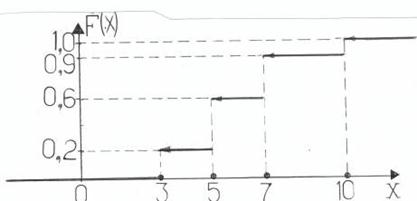
Рис.3.
Вероятность попадания случайной величины на заданный участок.
При решении практических задач, связанных со случайной величиной, часто оказывается необходимым вычислить вероятность того, что случайная величина примет значение, заключённое в некоторых пределах, например, 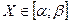 (см. рис. 4).
(см. рис. 4).

Рис. 4.
Очевидно, что 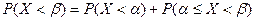 . Это же выражение можно запсать через функцию распределения:
. Это же выражение можно запсать через функцию распределения: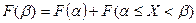 , откуда получим:
, откуда получим: 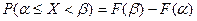 .
.
Вероятность попадания случайной величины на заданный участок равна приращению функции распределения на этом участке.
Будем «стягивать» участок в точку.
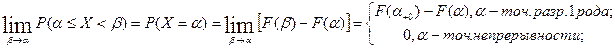
Если в точке 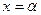 функция распределения имеет разрыв 1 рода (дискретная случайная величина), то предел равен значению скачка функции F(x) в точке х=
функция распределения имеет разрыв 1 рода (дискретная случайная величина), то предел равен значению скачка функции F(x) в точке х=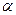 . Для непрерывной случайной величины предел равен нулю, т. е. вероятность любого конкретного значения непрерывной случайной величины равна нулю.
. Для непрерывной случайной величины предел равен нулю, т. е. вероятность любого конкретного значения непрерывной случайной величины равна нулю.
Плотность распределения непрерывной случайной величины.
|
|
|
Пусть дана непрерывная случайная величина Х с плотностью распределения F(x). Вероятность попадания случайной точки на элементарный промежуток 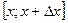 подсчитывается по полученной выше формуле:
подсчитывается по полученной выше формуле:
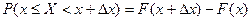 .
.
Поделим эту вероятность на 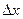 и рассмотрим предел отношения при
и рассмотрим предел отношения при 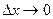 . При этом получим:
. При этом получим:
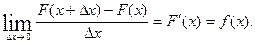
Определение. Предел отношения вероятности попадания непорерывной случайной величины Х на элементарный участок 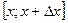 к длине этого участка
к длине этого участка 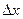 при стремлении
при стремлении 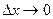 называется плотностью распределения случайной величины Х и обозначается символом f(x).
называется плотностью распределения случайной величины Х и обозначается символом f(x).
График функции f(x) наз. кривой распределения. Графики функции распределения F(x) и построенный по нему график плотности распределения f(x) приведены на рис. 5.
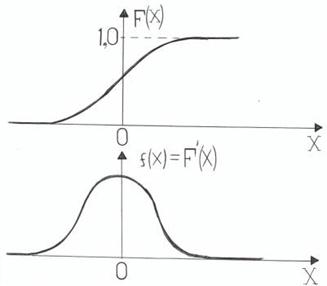
Рис.5.
Определение. Случайная величина Х называется непрерывной, если её функция распределения F(x) – непрерывна на всей числовой оси ОХ, а плотность распределения f(x) существует везде, за исключением, быть может, конечного числа точек разрыва 1 рода.
Отметим свойства плотности распределения.
1. 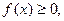 так как F(x) – неубывающая функция;
так как F(x) – неубывающая функция;
2. 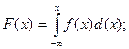 Докажем это. Рассмотрим элемент вероятности
Докажем это. Рассмотрим элемент вероятности
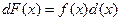 . Проинтегрируем это выражение:
. Проинтегрируем это выражение:
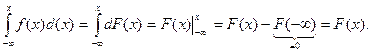
3.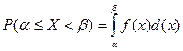 . Действительно,
. Действительно, 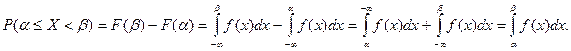
Иллюстрация свойства 3 приведена на рис. 6.
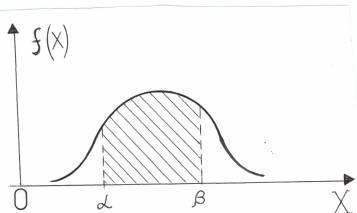
Рис. 6.
4. Очевидно, что для плотности распределения спораведливо соотношение: 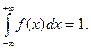
Функция распределения F(x) может быть задана как единая или составная функция, а так же может задаваться графически. Для непрерывной случайной величины график функции распределения всегда непрерывная линия, тогда как график плотности распределения может иметь одну или несколько точек разрыва первого рода.
Пример. Функция распределения непрерывной случайной величины Х задана выражением:
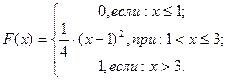
Найти плотность распределения. Построить график плотности распределения и вычислить вероятность попадания случайной точки в промежуток 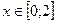 .
.
Решение.
График функции распределения задан составной функцией. Её вид приведен на рис. 6. Плотность распределения получаем дифференцированием функции распределения для каждого из указаных в условии задачи промежутков временни. Аналитическое выражение плотности распределения имеет вид:
|
|
|
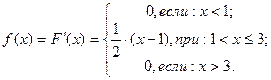
Графики функции распределения F(X) и плотности распределения F(x) приведены ниже (см. рис. 6). Геометрически график функции распределения выражает закон нарастания площади под графиком плотности распределения при увеличении текущего значения аргумента х. в пределе, при 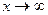 , эта площадь всегда становится равной 1. в данном примере график плотности распределения имеет одну точку разрыва первого рода при х = 3. Заштрихованная на нём площадь численно равна вероятности попадания случайной точки на указанный промежуток.
, эта площадь всегда становится равной 1. в данном примере график плотности распределения имеет одну точку разрыва первого рода при х = 3. Заштрихованная на нём площадь численно равна вероятности попадания случайной точки на указанный промежуток.
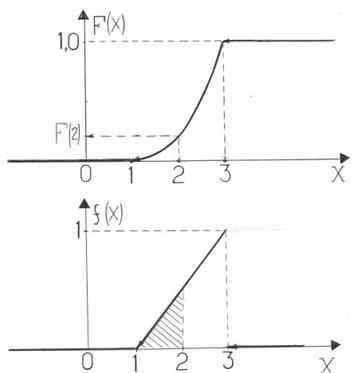
Рис. 6.
Вероятность попадания случайной точки на участок 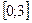 можно подсчитать двумя способами:
можно подсчитать двумя способами:
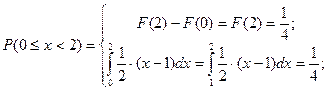
 2014-02-09
2014-02-09 1558
1558








