1. Теорема подобия Если 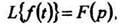 то для любого постоянного а > 0
то для любого постоянного а > 0
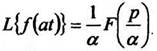 (4)
(4)
Пример 3. Найдем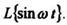 Из примера 2
Из примера 2 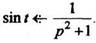 .По Формуле (4)
.По Формуле (4)
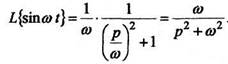
2.Дифференцирование оригинала Если 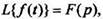 то
то
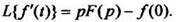 (5)
(5)
Методом индукции на основании формулы (5) получены формулы изображения высших производных:
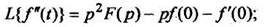 (6)
(6)
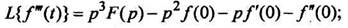 (7)
(7)
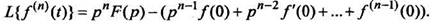 (8)
(8)
Пример 4. Определим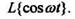 Так как
Так как 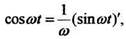
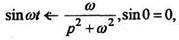 то по формуле (5) получим:
то по формуле (5) получим:
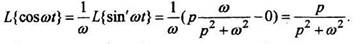
3. Дифференцирование изображения. Если 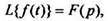 то
то
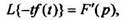 т.е. дифференцирование изображения сводится к умножению на
т.е. дифференцирование изображения сводится к умножению на 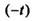 оригинала. В общем случае,
оригинала. В общем случае,
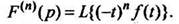 (9)
(9)
Пример 5. Определить изображения функций 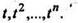
РЕШЕНИЕ
Так как 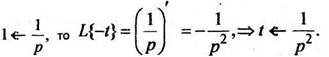
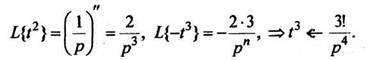
В общем случае 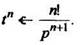
4. Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р:
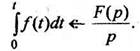 (10)
(10)
Пример 6. Найти изображение функци 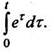
РЕШЕНИЕ Так как 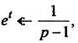 то по формуле (10)
то по формуле (10) 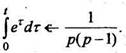
5. Интегрирование изображения. Интефирование изображения равносильно делению на t оригинала (если существует конечный предел 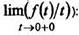
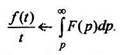 (11)
(11)
Пример 7. Найдем изображение функции 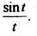
Так как 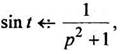 то по формуле (11) получаем
то по формуле (11) получаем
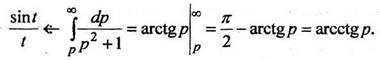
6. Теорема смещения При умножении оригинала на 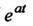 изображение получается смещение аргумента на
изображение получается смещение аргумента на 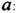
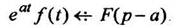 (12)
(12)
Пример 8. В примерах 3, 4, 5 найдены изображения функций 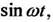
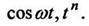 По формуле (12) находим:
По формуле (12) находим:
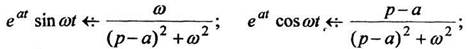
|
|
|
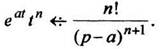
7. Теорема запаздывания. "Включение" оригинала с запаздыванием на 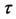 равносильно умножению изображения на
равносильно умножению изображения на 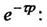
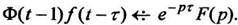 (13)
(13)
В данной формуле важно подчеркнуть, что функция 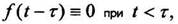 поэтому она умножена на единичную функцию Хевисайда с запаздыванием
поэтому она умножена на единичную функцию Хевисайда с запаздыванием 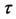 . График единичной функции Хевисайда с запаздывающим аргументом показан на рисунке 1.
. График единичной функции Хевисайда с запаздывающим аргументом показан на рисунке 1.
Изображение 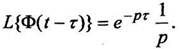
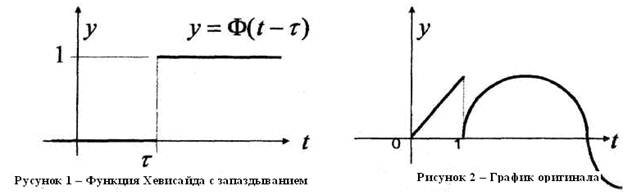
 2014-02-09
2014-02-09 3199
3199








