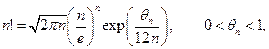
т.е.
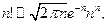
где 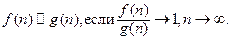
Определение. Подмножества 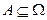 называются событиями и предполагается, что известны утверждения "исход
называются событиями и предполагается, что известны утверждения "исход 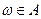 " или "исход
" или "исход 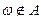 ".
".
Операции с событиями: объединение 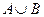 (или
(или 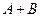 ), пересечение
), пересечение 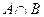 (или
(или 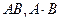 ), разность
), разность 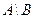 , отрицание
, отрицание 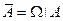 . Пустое множество обозначено
. Пустое множество обозначено  ; достоверное событие –
; достоверное событие – 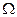 ;
; 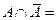 ;
; 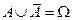 .
.
Определение. Алгебра 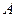 – это такая система подмножеств
– это такая система подмножеств 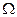 , что
, что
1) 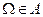
2) если 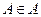 и
и 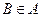 , то
, то 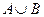 ,
, 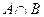 ,
, 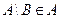 .
.
Примеры: 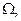 ,
, 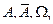 ,
, 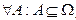 .
.
Определение. Разбиение 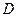 – система множеств
– система множеств 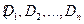 называется разбиением множества
называется разбиением множества 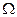 , если
, если
1) 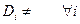 ,
,
2) 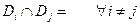 ,
,
3) 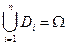
События 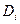 называются атомами разбиения.
называются атомами разбиения.
Если взять элементы 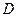 ,
,  и всевозможные объединения атомов, то получим алгебру
и всевозможные объединения атомов, то получим алгебру 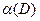 , порожденную разбиением
, порожденную разбиением 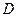 .
.
Разбиение 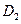 мельче
мельче 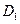 (
(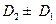 ), если
), если 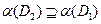 .
.
Каждому элементарному событию 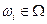 ,
, 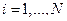 "припишем" меру (вес)
"припишем" меру (вес) 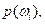 называемую вероятностью исхода
называемую вероятностью исхода 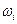 , если выполнены условия
, если выполнены условия
1) 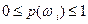 (неотрицательность)
(неотрицательность)
2) 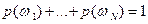 (нормированность).
(нормированность).
Тогда для любого события 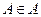 определим вероятность
определим вероятность 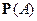 по формуле
по формуле
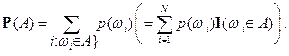
Определение. Тройка 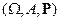 , где пространство элементарных событий
, где пространство элементарных событий 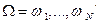 ,
, 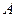 – некоторая алгебра подмножеств
– некоторая алгебра подмножеств 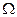 , вероятностная мера
, вероятностная мера 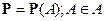 определяет конечное вероятностное пространство (вероятностную модель).
определяет конечное вероятностное пространство (вероятностную модель).
Свойства вероятности:
1) 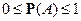
2) 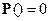
3) 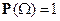
4) 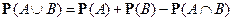 ,
,
если 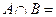 , то
, то 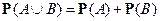
5) 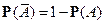
Пример 1. Биномиальное распределение.
n-кратное подбрасывание монеты с результирующим набором 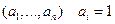 или
или 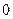 ,
, 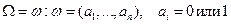 .
.
Припишем
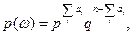
где 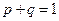 . Корректность следует из того, что если
. Корректность следует из того, что если 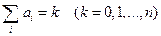 , то
, то 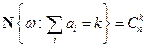 и
и
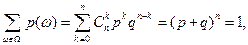
т.е.
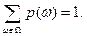
Если 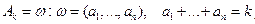 , то
, то 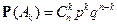 .
.
Набор 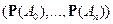 называется биномиальным распределением.
называется биномиальным распределением.
Пример 2. Случайное блуждание.
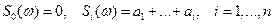 .
.
Определение. Условной вероятностью события 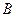 при условии
при условии 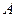 с
с 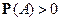 называется
называется
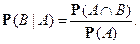
В классическом случае
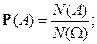
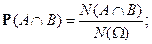
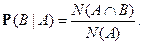
Свойства условной вероятности:
1) 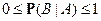
2) 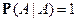
3) 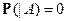
4) 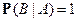 при
при 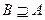
5) 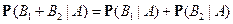 при
при 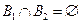 ,
,
следовательно, 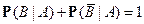 .
.
Пусть 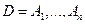 – разбиение и пусть
– разбиение и пусть 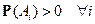 и, следовательно,
и, следовательно, 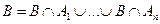 ,
, 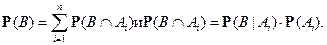 Следовательно, верна
Следовательно, верна
формула полной вероятности:
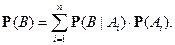
Если 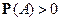 и
и 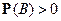 , то
, то 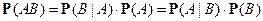 . Отсюда получаем
. Отсюда получаем
формулу Байеса:
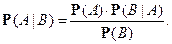
Если 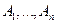 – разбиение с
– разбиение с 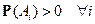 , то очевидна
, то очевидна
теорема Байеса:
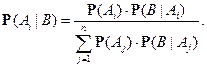
Определение. События 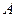 и
и 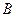 называются независимыми, если
называются независимыми, если
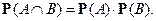
Определение. Алгебры 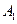 и
и 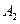 называются независимыми, если попарно независимы любые два множества
называются независимыми, если попарно независимы любые два множества 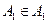 и
и 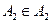 .
.
Определение. Множества 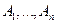 – называются независимыми в совокупности (или просто независимыми), если для любого
– называются независимыми в совокупности (или просто независимыми), если для любого 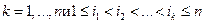
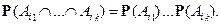
Алгебры множеств 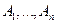 называются независимыми в совокупности, если независимы любые множества
называются независимыми в совокупности, если независимы любые множества 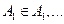 ,
, 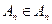 .
.
Из попарной независимости не следует независимость в совокупности.
Пример. 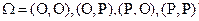 ,
, 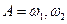 ,
, 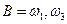 ,
, 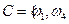 ,
, 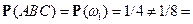
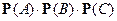 , но
, но 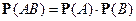 ,
, 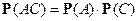 ,
, 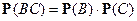 .
.
Пусть 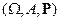 – вероятностное пространство с конечным числом исходов,
– вероятностное пространство с конечным числом исходов, 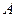 – алгебра всех возможных подмножеств
– алгебра всех возможных подмножеств 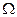 .
.
Определение. Всякая числовая функция 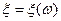 , определенная на конечном пространстве элементарных событий
, определенная на конечном пространстве элементарных событий 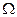 , называется (простой) случайной величиной.
, называется (простой) случайной величиной.
Пример.
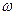
| OO | OP | PO | PP |
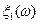
| ||||
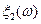
| -2 | |||
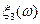
| ||||
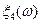
| ||||
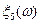
| ||||
| … | … | … | … | … |
Пусть 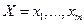 – все возможные значения
– все возможные значения 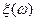 ,
, 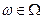
(очевидно, 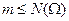 ), и пусть
), и пусть 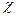 – совокупность подмножеств
– совокупность подмножеств 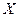 .
.
На 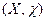 вероятность
вероятность 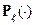 индуцирована
индуцирована  – по формуле
– по формуле 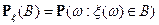 ,
, 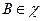 , и определяется по формуле
, и определяется по формуле 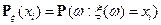 ,
, 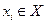 .
.
Определение. Набор 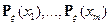 - называется распределением вероятностей случайной величины
- называется распределением вероятностей случайной величины  .
.
Пример. Биномиальная случайная величина  с n+1 значениями
с n+1 значениями 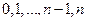 с вероятностями
с вероятностями 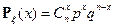 ,
, 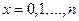 .
.
Определение. Пусть 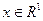 . Функция
. Функция 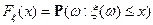 называется функцией распределения случайной величины
называется функцией распределения случайной величины  , если
, если
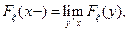
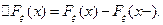
Наряду со случайными величинами рассматриваются случайные вектора (пусть здесь – вектора-столбцы) 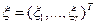 ,
, 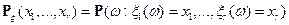 – распределения вероятностей случайного вектора
– распределения вероятностей случайного вектора  .
.
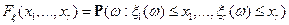 – функция распределения случайного вектора
– функция распределения случайного вектора  .
.
Определение. Случайные величины 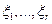 – независимы (т.е. независимы в совокупности), если для любого
– независимы (т.е. независимы в совокупности), если для любого 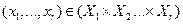
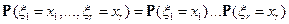
или, что то же самое
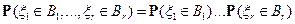
для любых 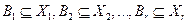 .
.
Если  и
и 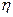 – независимые случайные величины, то для
– независимые случайные величины, то для 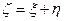 имеет место формула свёртки
имеет место формула свёртки
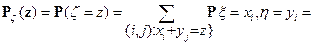
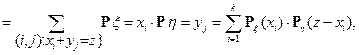
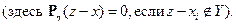
Пусть 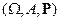 – конечное вероятностное пространство,
– конечное вероятностное пространство, 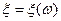 – некоторая случайная величина со значениями в
– некоторая случайная величина со значениями в 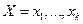 . Пусть
. Пусть 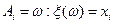 ,
, 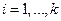 . Тогда
. Тогда
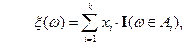
где 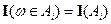 – индикаторная функция,
– индикаторная функция, 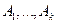 – разбиение.
– разбиение.
Справедливо следующее
Определение. Математическим ожиданием (или средним) случайной величины 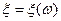 называют число
называют число 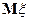
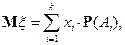
или
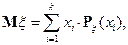
или
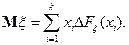
Заметим, что в элементарном (конечном) случае (из равенства интегралов Лебега-Стильтьеса и Римана-Стильтьеса в данном случае)
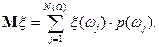
 2014-02-12
2014-02-12 638
638








