Докажем 2).
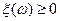 , следовательно,
, следовательно,
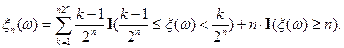
Очевидно, что
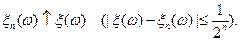
Докажем 1)
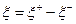 , где
, где 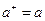 при
при 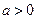 и
и 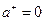 при
при 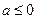 ;
; 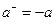 при
при 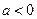 ,
, 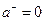 при
при 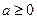 .
.
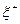 и
и 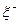 неотрицательные и для каждой по 2) существуют последовательности случайных величин такие, что
неотрицательные и для каждой по 2) существуют последовательности случайных величин такие, что 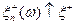 и
и 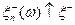 и, следовательно,
и, следовательно, 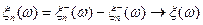 и
и 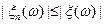 . Теорема доказана.
. Теорема доказана.
4. Математическое ожидание
Если 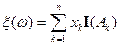 , то
, то 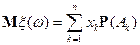 .
.
Пусть 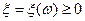 – неотрицательная случайная величина. Построим последовательность простых случайных величин
– неотрицательная случайная величина. Построим последовательность простых случайных величин 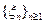 таких что
таких что
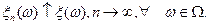
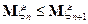 , следовательно,
, следовательно, 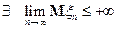 .
.
Определение. Математическим ожиданием 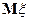 при
при 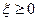 назовем
назовем 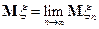 .
.
Определение. Пусть 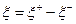 и пусть
и пусть 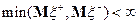 , тогда математическое ожидание
, тогда математическое ожидание 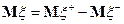 .
.
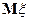 конечно, если
конечно, если 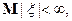
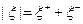 , следовательно,
, следовательно,
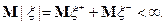
 2014-02-12
2014-02-12 335
335








