Определение. Координатами точки М на плоскости в декартовой системе координат (О, e 1, e 2) называются координаты ее радиус-вектора 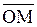 в базисе e 1, e 2.
в базисе e 1, e 2.
Таким образом, чтобы найти координаты точки М, нужно разложить вектор 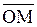 по базису e 1, e 2:
по базису e 1, e 2:
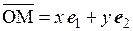 ,
,
тогда числа х и у будут координатами точки М в выбранной системе координат. В силу рассмотренной выше теоремы о разложении вектора по базису такое разложение единственно; в выбранном базисе положение точки однозначно определяется парой чисел (х, у) – координатами точки. Координату х называют абсциссой точки М, координату у – ординатой точки М.
Определение. Координатами вектора a на плоскости в декартовой системе координат (О, e 1, e 2) называют координаты этого вектора в базисе e 1, e 2.
Другими словами, чтобы найти координаты вектора a, нужно разложить его по базису e 1, e 2:
a =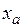 e 1+
e 1+  e 2;
e 2;
тогда коэффициенты 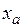 и
и  будут координатами вектора a в декартовой системе координат (О, e 1, e 2).
будут координатами вектора a в декартовой системе координат (О, e 1, e 2).
Среди декартовых систем координат простейшей является прямоугольная декартова система координат.
|
|
|
Определение. Декартова система координат (О, e 1, e 2) на плоскости называется прямоугольной, если e 1 и e 2 – взаимно перпендикулярные единичные векторы.
Базисные векторы e 1, e 2 прямоугольной декартовой системы координат на плоскости представляют собой ортонормированный базис евклидова пространства R2.
Две взаимно перпендикулярные прямые, проходящие через О и параллельные соответственно векторам e 1 и e 2, называют осями координат. Первую из них обычно называют осью абсцисс и обозначают Ох, вторую – осью ординат и обозначают Оу. Единичные векторы оси Ох и оси Оу, равные базисным векторам e 1и e 2, соответственно, обычно обозначают  . Декартову прямоугольную систему координат на плоскости будем обозначать Оху.
. Декартову прямоугольную систему координат на плоскости будем обозначать Оху.
Определим операции над векторами, заданными координатами в декартовой прямоугольной системе координат, в соответствии с правилами, определенными для векторов векторного пространства.
Пусть даны точки 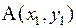 и
и  . Найдем координаты вектора
. Найдем координаты вектора 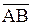 . Имеем
. Имеем 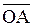 =
=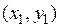 ,
,  =
=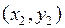 , или
, или 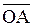 =
=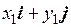 ,
,  =
= . Вычитая из второго равенства первое, получаем
. Вычитая из второго равенства первое, получаем
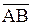 =
= –
–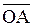 =
= –(
–(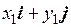 )=
)= .
.
Таким образом, координаты вектора 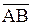 =(
=(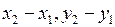 ).
).
Произведением вектора 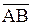 =(
=(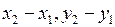 ) на число k будет вектор k
) на число k будет вектор k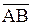 =
=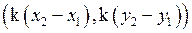 .
.
Скалярное произведение двух векторов в декартовой прямоугольной системе координат можно определить по формуле (1.19) или по формуле (1.14). Формула (1.10) дает возможность вычислить угол между векторами.
Расстояние между точками А и В на плоскости можно интерпретировать как длину вектора 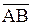 , поэтому
, поэтому
АВ=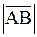 =
= =
=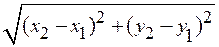 .
.
Пример. Даны точки А(1,–3) и В(–2,1). Вычислить угол, который вектор 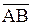 составляет с положительным направлением оси Оу.
составляет с положительным направлением оси Оу.
○ Положительное направление оси Оу определяется единичным вектором этой оси 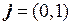 . Найдем координаты и длину вектора
. Найдем координаты и длину вектора 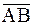 :
:
|
|
|
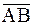 =
=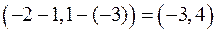 ; АВ=
; АВ=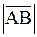 =
=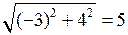 .
.
Скалярное произведение векторов 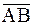 и
и 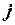 найдем по формуле (1.19): (
найдем по формуле (1.19): (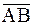 ,
,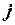 )= –3×0+4×1=4. Теперь по формуле (1.10) находим угол между векторами
)= –3×0+4×1=4. Теперь по формуле (1.10) находим угол между векторами 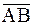 и
и 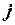 :
: 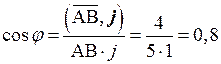 ;
; 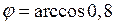 . ●
. ●
 2014-02-12
2014-02-12 1144
1144







