В матрице определителя n-го порядка вычеркнем 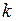 -ю строку и
-ю строку и 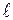 -ый столбец:
-ый столбец:

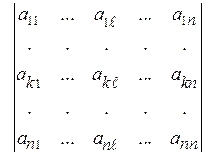
Оставшийся определитель (n–1)-го порядка называется минором
(n–1)-го порядка элемента 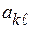 определителя n-го порядка и обозначается
определителя n-го порядка и обозначается 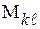 .
.
Определение. Алгебраическим дополнением 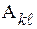 элемента определителя n-го порядка называется произведение минора
элемента определителя n-го порядка называется произведение минора 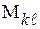 элемента
элемента 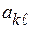 на
на 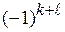 , т.е.
, т.е. 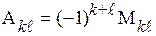 .
.
Пример. Найти минор и алгебраическое дополнение элемента 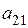 определителя
определителя 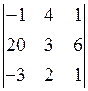 .
.
○ Вычеркнем 2-ю строку и 1-й столбец определителя. Получим минор 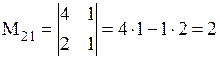 , алгебраическое дополнение
, алгебраическое дополнение 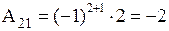 . ●
. ●
Для вычисления определителей большое значение имеет следующая теорема.
Теорема 3.4. Определитель n-го порядка равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения, т.е.
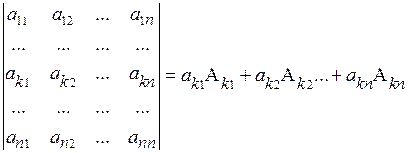 . (3.7)
. (3.7)
Формула (3.7) называется разложением определителя по элементам k-ой строки. Разложение определителя по элементам какого-либо столбца записывается аналогично.
Формула (3.7) сводит вычисление определителя n-го порядка к вычислению n определителей (n–1)-го порядка. Зная формулу (3.6) вычисления определителя третьего порядка, мы, например, можем найти определитель четвертого порядка путем разложения его на сумму алгебраических дополнений по формуле (3.7).
|
|
|
Пример. Вычислить определитель четвертого порядка
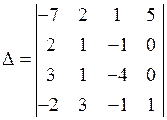 .
.
○ Разложить определитель можно по любой строке или любому столбцу, согласно формуле (3.7). Однако если выбрать такую строку (или столбец), в которой больше элементов, равных нулю, то объем вычислений можно существенно уменьшить. В нашем случае наиболее подходящим является четвертый столбец. Разложение определителя по этому столбцу имеет вид
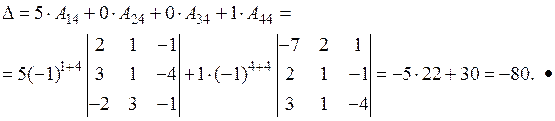
Теорема 3.5. Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответственных элементов другой строки (столбца) равна нулю.
□ Покажем, например, что
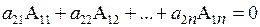
Для каких угодно чисел 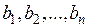 имеет место равенство
имеет место равенство
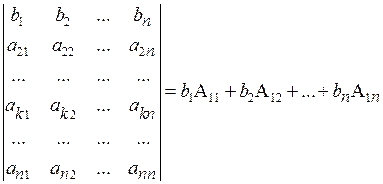 .
.
Здесь записана формула разложения определителя по первой строке. Полагая 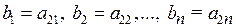 , находим
, находим
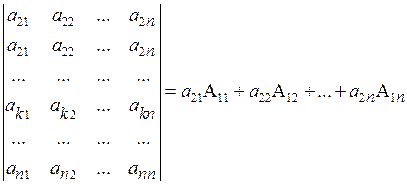 .
.
Стоящий слева определитель содержит две одинаковые строки – первую и вторую, поэтому равен нулю. Значит 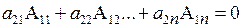 и равенство (3.7) доказано. ■
и равенство (3.7) доказано. ■
 2014-02-12
2014-02-12 679
679








