Основные понятия теории графов
ТОПОЛОГИЧЕСКОЕ ОПИСАНИЕ СХЕМ
Под математической моделью понимают совокупность уравнений, описывающих цепь, решение которых позволяет определить ее характеристики. В качестве математических моделей обычно выступают системы линейных, нелинейных алгебраических либо дифференциальных уравнений. В основе методов формирования математических моделей цепей лежит совокупность топологических и компонентных уравнений.
Топологию схем удобно описывать на языке теории графов, имеющей множество инженерных приложений. Топология схемы несет информацию о соединении элементов. Топологические уравнения цепи являются формой записи основных топологических законов (первый и второй законы Кирхгофа). Компонентные уравнения представляют собой запись законов Ома для компонентов - элементов схемы.
Для описания топологии цепи каждый двухполюсный элемент замещается направленным отрезком линии, называемым ветвью графа. Соединение двух и более ветвей в точке называется узлом или вершиной графа. Пронумеруем ветви и узлы электрической схемы и соответствующего ей графа.
Сформулируем законы Кирхгофа для электрических цепей.
Закон Кирхгофа для напряжений: сумма падений напряжений вдоль любого замкнутого контура цепи равна нулю.
Законы Кирхгофа для токов:
1. Алгебраическая сумма токов, втекающих в узел и вытекающих из узла, равна нулю.
2. В любом сечении, разделяющем цепь на две части, алгебраическая сумма токов, протекающих по соединительным ветвям через сечение, равна нулю.
Направления отрезков линий (токов) пассивных ветвей можно выбирать произвольно, однако условимся, что для источников тока направление совпадает с истинным, а для источников напряжения направлено против ЭДС.Узлы схемы нумеруются в произвольном порядке непрерывной последовательностью цифр, общий (заземленный узел) обычно считается нулевым.
Матрица инциденций. Применение закона Кирхгофа для токов в узлах позволяет получить матрицу инциденций, отображающую топологические свойства цепи. Рассмотрим простую цепь и соответствующий ей граф (рисунок 2.1).
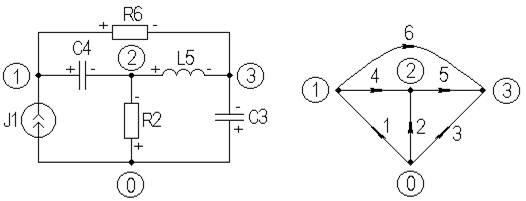
Рисунок 2.1 – Электрическая цепь и ее направленный граф
Запишем закон Кирхгофа для токов в узлах:
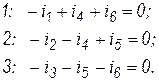
Этиуравнения можно записать в матричной форме
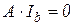 , (2.1)
, (2.1)
где 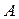 - матрица инциденций.
- матрица инциденций.
Для рассматриваемого примера матрица 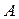 имеет вид:
имеет вид:
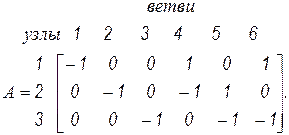

Матрица содержит 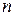 строк и
строк и 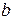 столбцов, где
столбцов, где 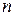 - число независимых (незаземленных) узлов;
- число независимых (незаземленных) узлов; 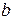 - число ветвей графа. Строки матрицы указывают ветви, инцидентные соответствующему узлу, и их направленность. Столбцы матрицы указывают узлы, инцидентные соответствующей ветви и порядок обхода.
- число ветвей графа. Строки матрицы указывают ветви, инцидентные соответствующему узлу, и их направленность. Столбцы матрицы указывают узлы, инцидентные соответствующей ветви и порядок обхода.
Напряжения ветвей и узловые потенциалы также связаны через матрицу инциденций соотношением, отвечающим закону Кирхгофа для напряжений
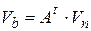 , (2.2)
, (2.2)
где 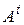 - транспонированная матрица инциденций;
- транспонированная матрица инциденций; 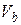 - напряжение ветвей,
- напряжение ветвей, 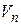 - напряжения узлов.
- напряжения узлов.
Матрицы сечений и контуров. Изобразим на рисунке 2.2 граф предыдущей цепи, но с тремя сечениями. Положительное направление сечений укажем стрелками.
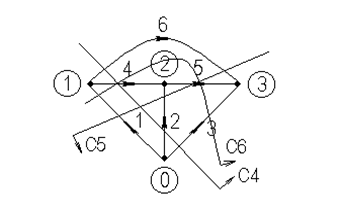
Рисунок 2.2 – Граф схемы с сечениями
Составим уравнения для токов сечений:
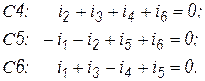
Возникает вопрос: сколько необходимо иметь уравнений для определения всех токов и напряжений цепи? Для ответа следует воспользоваться понятием дерева графа.
Деревом связанного графа называется связанный подграф, включающий все узлы графа, но не содержащий замкнутых контуров. Ветви, не вошедшие в дерево графа, образуют дополнение дерева графа. Дерево графа цепи с (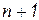 ) узлами имеет
) узлами имеет 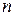 ветвей. Ветви графа, входящие в дерево, называются ребрами. Ветви дополнения графа называются хордами.
ветвей. Ветви графа, входящие в дерево, называются ребрами. Ветви дополнения графа называются хордами.
Главным сечением графа называют сечение, проходящее через одно ребро и произвольное число хорд. Т.к. в дерево входит только 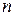 ветвей, то существует
ветвей, то существует 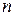 главных сечений, что соответствует
главных сечений, что соответствует 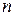 независимым уравнениям для токов.
независимым уравнениям для токов.
Нумерация ветвей и узлов схемы представляет произвольную процедуру и диктуется соображениями удобства. Многие выкладки существенно упростятся, если:
1) выбираем направления ветвей;
2) выбираем дерево графа;
3) нумеруем ветви графа, вначале ребра, затем хорды.
На рисунке 2.3 изображен один из вариантов такого выбора. Уравнения для токов сечений в этом случае будут следующими:
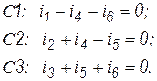
Рисунок 2.3 – Граф схемы с выделенным деревом
В матричной форме эти уравнения можно записать в виде
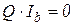 , (2.3)
, (2.3)
где
|
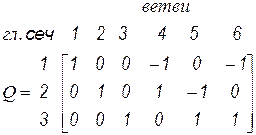
- матрица главных сечений (МГС). Направление сечения определяется направлением соответствующего ребра. Строки матрицы указывают относительное направление рассеченных ветвей. Столбцы матрицы указывают сечение, проходящеечерез ветвь, и относительное направление. Напряжения ветвей можно выразить через напряжения ребер соотношением
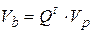 . (2.4)
. (2.4)
Рассмотрим, как изменится вид матрицы Q при другом выборе дерева графа и направлений его ветвей для той же цепи рисунок 2.4.
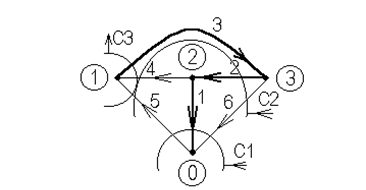
Рисунок 2.4 – Граф схемы с другим деревом
Если будем следовать указанным правилам нумерации ветвей графа, то получим матрицу Q следующего вида
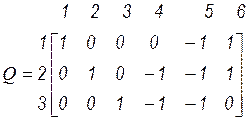 .
.
В обоих случаях подматрица, соответствующая дереву графа, является единичной. Следовательно, матрицу Q можно записать как
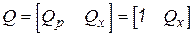 , (2.5)
, (2.5)
где 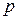 соответствует ребрам, а
соответствует ребрам, а 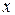 - хордам. Ранг матрицы
- хордам. Ранг матрицы 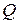 равен
равен 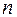 . Из соотношений (2.3) и (2.5) следует
. Из соотношений (2.3) и (2.5) следует
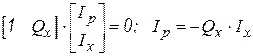 . (2.6)
. (2.6)
Использование закона Кирхгофа для напряжений приводит к другому описанию топологических свойств цепи, основанному на контурах. Ограничимся рассмотрением простых контуров, не проходящих два и более раз через одну ветвь или узел.
Для упрощения записи системы контурных уравнений будем придерживаться следующего порядка:
1. Пронумеруем ребра и хорды графа, как было предложено ранее.
2. Переберем хорды в соответствии с их номерами и пронумеруем контура, начиная с единицы.
3. Направление обхода контура выбираем совпадающим с направлением образующей хорды.
Запишем контурные уравнения для графов схемы, приведенных на рис. 2.3, 2.4.
Для первого графа с учетом нумерации ветвей

Для второго графа –
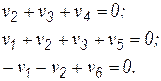
В матричной форме эти уравнения имеют вид
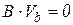 , (2.7)
, (2.7)
где 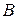 - матрица контуров.
- матрица контуров.
Токи ветвей выражаются через токи хорд (контуров) соотношением
 . (2.8)
. (2.8)
Матрица B называется матрицей главных контуров (МГК). Вид матриц для указанных графов с выбранными деревьями следующий:
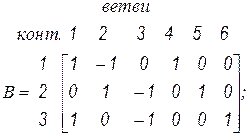
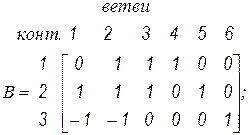
Ранг матрицы 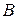 равен (
равен (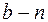 ). Строки матрицы указывают ветви, образующие данный контур, и их направленность. Столбцы матрицы указывают контуры, проходящие через ветвь, и их направленность. Видим, что подматрицы
). Строки матрицы указывают ветви, образующие данный контур, и их направленность. Столбцы матрицы указывают контуры, проходящие через ветвь, и их направленность. Видим, что подматрицы 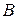 , соответствующие дополнению дерева, есть единичные матрицы. В результате можно записать
, соответствующие дополнению дерева, есть единичные матрицы. В результате можно записать
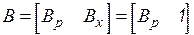 . (2.9)
. (2.9)
Из соотношений (2.7), (2.9) следует
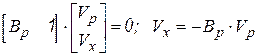 . (2.10)
. (2.10)
 2014-02-12
2014-02-12 6884
6884







