Пусть x* 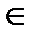 locmin f
locmin f 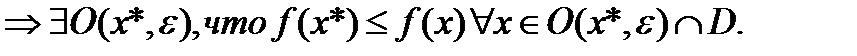
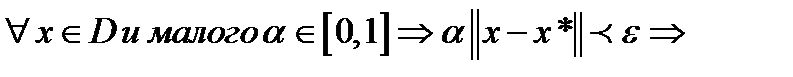 (из выпуклости D)
(из выпуклости D) 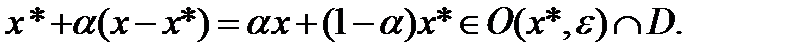 Из выпуклости
Из выпуклости 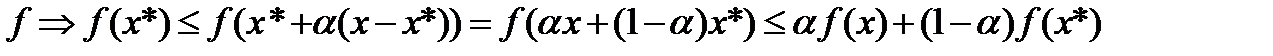 или
или
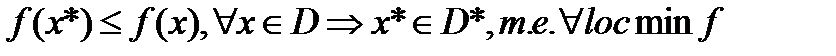 является глобальным.
является глобальным.
Пусть 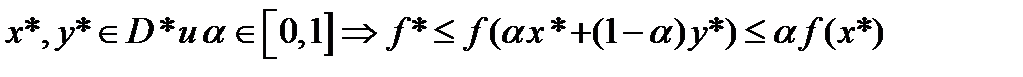
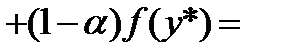
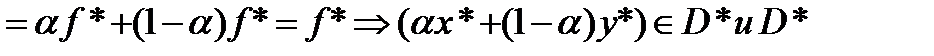 -выпукло. Если
-выпукло. Если 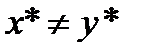 ,то для строго выпуклых функций предыдущее неравенством не может превратиться в равенство и они не могут достигать минимум более чем в одной точке.
,то для строго выпуклых функций предыдущее неравенством не может превратиться в равенство и они не могут достигать минимум более чем в одной точке.
Теорема 2. Если 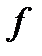 выпукла на выпуклом множестве D и
выпукла на выпуклом множестве D и 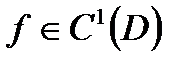 то
то 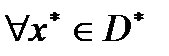
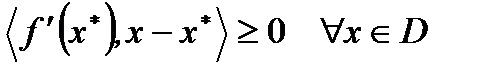 (1) и если
(1) и если 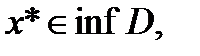 то (1) превращается в равенство. Если кроме того
то (1) превращается в равенство. Если кроме того 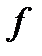 выпукла на D, то (1)является достигнутым условием, чтобы
выпукла на D, то (1)является достигнутым условием, чтобы 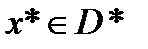 .Для недифференцируемых функций критерий
.Для недифференцируемых функций критерий 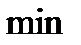 вводится с использованием понятия субградиента.
вводится с использованием понятия субградиента.
Опр.1. Пусть 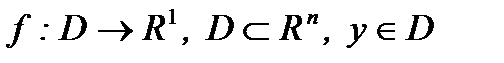 . Вектор
. Вектор 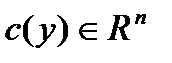 называется субградиентом
называется субградиентом 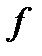 в
в 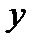 , если
, если 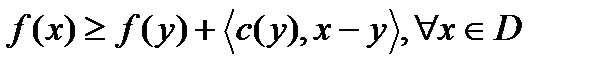 . (2)
. (2)
Замечание: множество всех субградиентов 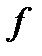 в
в 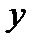 и обозначается
и обозначается 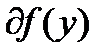 , а (2) означает, что график
, а (2) означает, что график 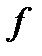 лежит не ниже графика линейной функции
лежит не ниже графика линейной функции 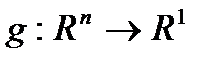 , определенной равенством
, определенной равенством 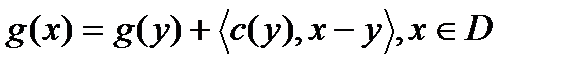 .
.
Теорема 3. Если 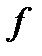 выпукла на выпуклом
выпукла на выпуклом 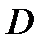 и
и 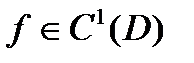 , то
, то 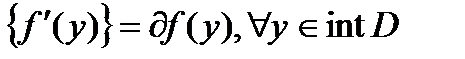 .
.
Доказательство:
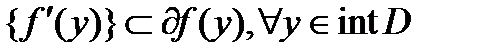 (следует из Т1, п.3.2). Обратное вложение: т.к.
(следует из Т1, п.3.2). Обратное вложение: т.к. 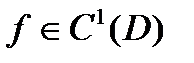 и из (2)
и из (2) 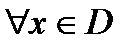 и
и 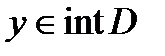 выполняется
выполняется 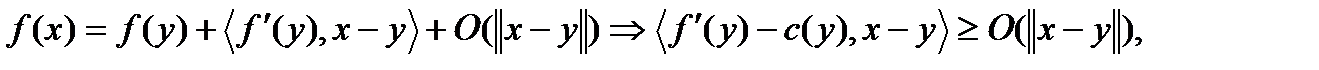 (3)
(3)
а условие 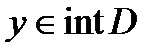 влечет
влечет 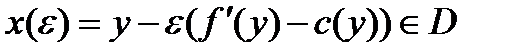 для всех малых
для всех малых 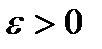 , и подставляя
, и подставляя 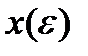 в (3) получаем
в (3) получаем 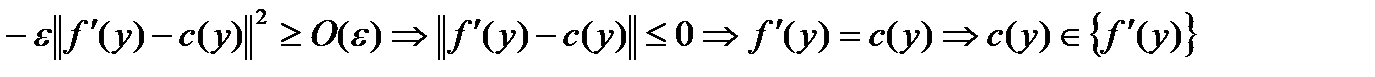 . ч.т.д.
. ч.т.д.
Замечание: субдифференциал не пуст в каждой точке области определения выпуклой функции.
Теорема 4: Пусть 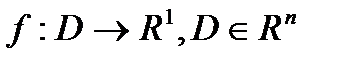 . Точка
. Точка 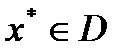 является точкой
является точкой 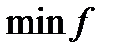 на
на 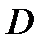
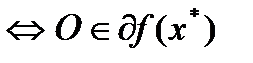 .
.
Док-во:
Неравенство 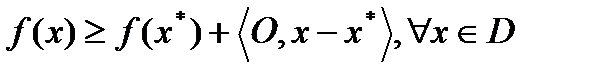 (4) имеет место, если
(4) имеет место, если 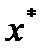 - точка
- точка 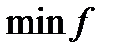 на
на 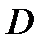 . Оно влечет за собой
. Оно влечет за собой 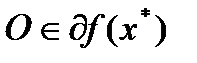 . Обратно, условие (4) означает, что
. Обратно, условие (4) означает, что  принадлежит субдифференциалу
принадлежит субдифференциалу 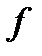 в
в 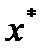 . Это означает, что
. Это означает, что 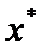 - точка
- точка 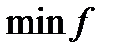 на
на 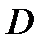 .
.
10. Функция Лагранжа и седловая точка.
Пусть 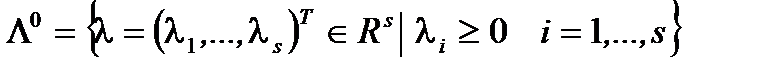
Опр.1. 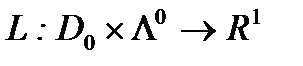 определенная формулой
определенная формулой 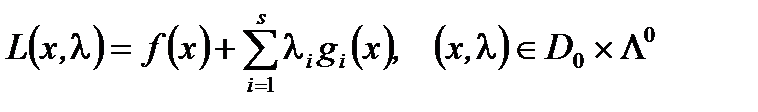 называется регулярной функцией Лагранжа для задачи выпуклого программирования (ВП).
называется регулярной функцией Лагранжа для задачи выпуклого программирования (ВП).
Опр. 2. Пара 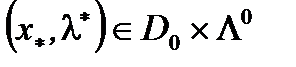 называется Седловой точкой для задачи ВП, если
называется Седловой точкой для задачи ВП, если 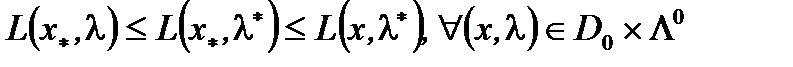 (1)
(1)
Теорема 1. 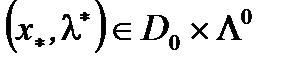 седловая точка для
седловая точка для 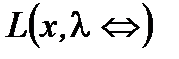
1) 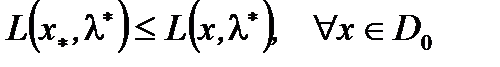 ,
,
2) 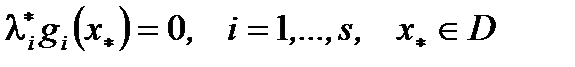
 2015-01-21
2015-01-21 546
546








