Пользуясь Теоремой о среднем, получим следующие формулы для конечных приращений функции 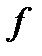 :
:
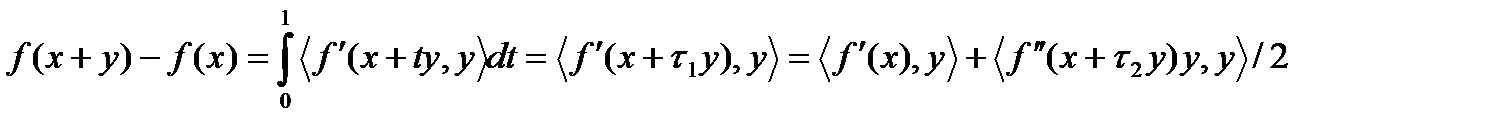 , где
, где 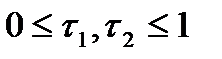
Воспользуемся условием сильной выпуклости 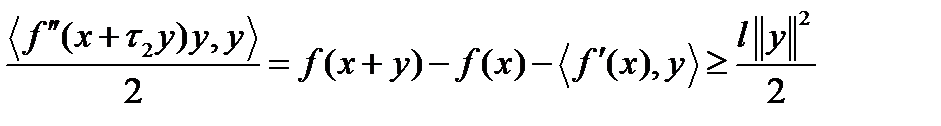
Заменяя 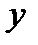 на
на 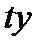 , получим:
, получим: 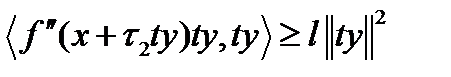 .Следовательно,
.Следовательно, 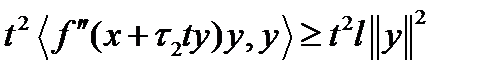 .
.
Поделив на 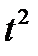 и устремив
и устремив 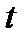 к нулю, будем иметь
к нулю, будем иметь 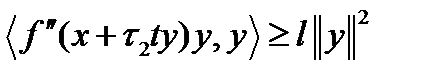 .
.
Положим 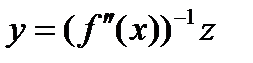 и, используя неравенство Коши-Буняковского, получим
и, используя неравенство Коши-Буняковского, получим 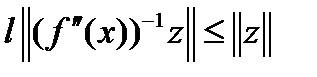 для любого
для любого 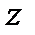 . Это означает, что
. Это означает, что 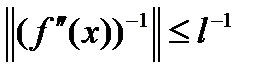 . Лемма доказана.
. Лемма доказана.
Пусть последовательность 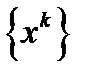 получена с помощью метода Ньютона и точка
получена с помощью метода Ньютона и точка 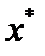 - глобальный минимум функции
- глобальный минимум функции 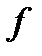 . Нижеследующая теорема устанавливает условия квадратичной скорости сходимости метода.
. Нижеследующая теорема устанавливает условия квадратичной скорости сходимости метода.
Теорема 1. Пусть дважды непрерывно дифференцируемая функция 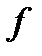 сильно выпукла (с константой
сильно выпукла (с константой 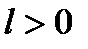 ), а вторая производная удовлетворяет условию Липшица
), а вторая производная удовлетворяет условию Липшица 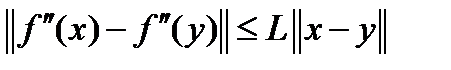 , для любых
, для любых 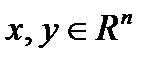 , и
, и 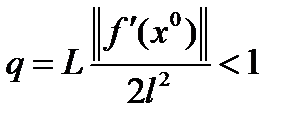 . Тогда
. Тогда 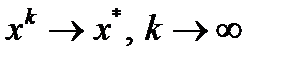 и метод Ньютона имеет квадратичную скорость сходимости
и метод Ньютона имеет квадратичную скорость сходимости 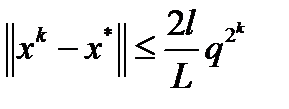 .
.
 2015-01-21
2015-01-21 519
519








