2015-01-21
780
Рассмотрим управляемую систему, движение которой описывается уравнением (*) п.17.1. Требуется перевести систему за время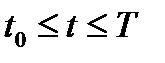 
из состояния 
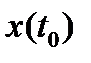в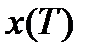 
так, чтобы в 
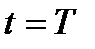выполнялось x(t)=x(T) и имел место расход усилий на управление в количестве 
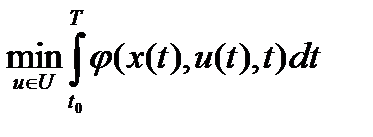. Решение неоднозначного уравнения может быть записано как сумма общего решения однородного и частного неоднородного. Оно может быть записано в виде:
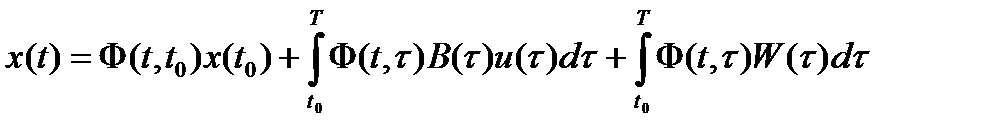и при t=T
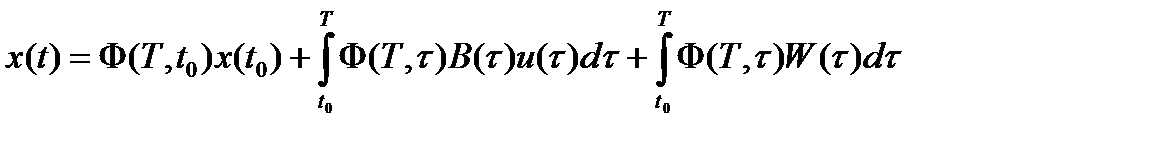, или 
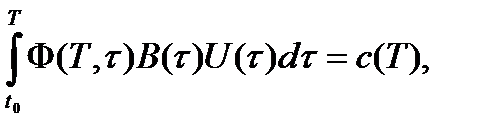где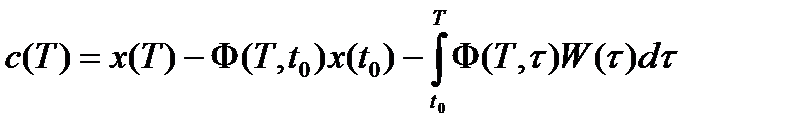 
, 
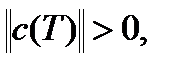
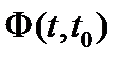- фундаментальная матрица Коши. Исходная задача уравнения системой свелась к изопериметрической задаче вариационного исчисления: Найти вектор-функцию 
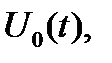обеспечивающую 
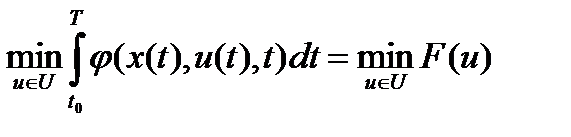при ограничениях 
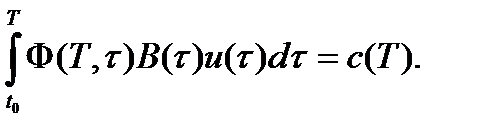Принцип относительности ее решения формулируется теоремой:
Теорема1 (Крейна). В пространстве U существует линейный функционал F(u), для которого выполняется условие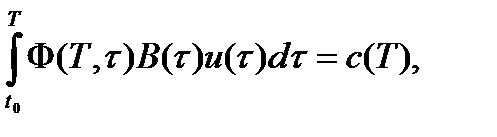 
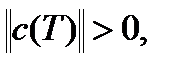и который имеет минимальную норму 
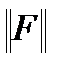при условии 
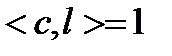для любых компонент вектора 
.
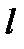Доказано, что если в качестве критериального функционала принимается величина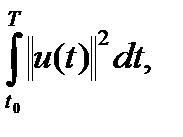 
то оптимальная операция, выражающейся минимальной функцией 
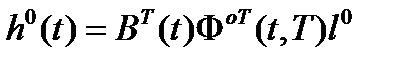удовлетворяет условию 
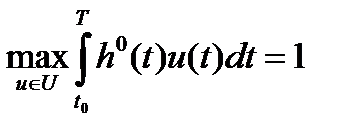и тогда 
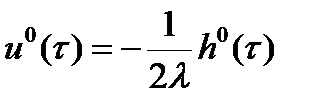, где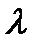 
- множитель Лагранжа, 
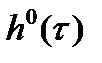- вектор-столбец.
|
|
|
Замечание. Математическое содержание задачи представляет собой известную проблему моментов.
