Рассмотрим поток событий, обладающий всеми тремя свойствами: стационарный, без последействия, ординарный. Такой поток называется простейшим (или стационарным пуассоновским) потоком. Название «простейший» связано с тем, что математическое описание событий, связанных с простейшими потоками, оказывается наиболее простым. Отметим, между прочим, что «самый простой», на первый взгляд, регулярный поток со строго постоянными интервалами между событиями отнюдь не является «простейшим» в вышеназванном смысле слова: он обладает ярко выраженным последействием, так как моменты появления событий связаны между собой жесткой функциональной зависимостью. Именно из-за этого последействия анализ процессов, связанных с регулярными потоками, оказывается, как правило, труднее, а не легче по сравнению с простейшими.
Простейший поток играет среди других потоков особую роль — можно доказать, что при суперпозиции (взаимном наложении) достаточно большого числа потоков, обладающих последействием (лишь бы они были стационарны и ординарны), образуется суммарный поток, который можно считать простейшим, и тем точнее, чем большее число потоков суммируется. Дополнительно требуется, чтобы складываемые потоки были сравнимы по интенсивности, т. е., чтобы среди них не было, скажем, одного, превосходящего по интенсивности сумму всех остальных.
Если поток событий не имеет последействия, ординарен, но не стационарен, он называется нестационарным пуассоновским потоком. В таком потоке интенсивность 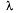 (среднее число событий в единицу времени) зависит от времени:
(среднее число событий в единицу времени) зависит от времени:
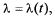
тогда как для простейшего потока
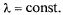
Пуассоновский поток событий (как стационарный, так и нестационарный) тесно связан с известным распределением Пуассона — число событий потока, попадающих на любой участок, распределено по закону Пуассона.
Поясним, что это означает. Рассмотрим на оси t, где наблюдается поток событий, некоторый участок времени длины 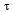 (см. рис. 5.3, а), начинающийся в момент
(см. рис. 5.3, а), начинающийся в момент 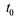 и заканчивающийся в момент
и заканчивающийся в момент 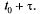 Нетрудно доказать (доказательство дается во всех курсах теории вероятностей), что вероятность попадания на этот участок ровно т событий и выражается формулой:
Нетрудно доказать (доказательство дается во всех курсах теории вероятностей), что вероятность попадания на этот участок ровно т событий и выражается формулой:
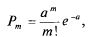 (5.15)
(5.15)
где а — среднее число событий, приходящееся на участок 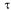 ; е — основание натуральных логарифмов.
; е — основание натуральных логарифмов.
Для стационарного (простейшего) пуассоновского потока величина а равна интенсивности потока, умноженной на длину интервала:
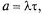
т. е. не зависит от того, где на оси t находится период 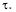 Для нестационарного пуассоновского потока величина а зависит от того, в какой точке
Для нестационарного пуассоновского потока величина а зависит от того, в какой точке 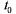 начинается участок t.
начинается участок t.
Рассмотрим на оси t простейший поток событий с интенсивностью 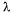 (рис. 5.3, б). Нас будет интересовать случайный интервал времени Т между соседними событиями в этом потоке; найдем его закон распределения. Сначала найдем функцию распределения:
(рис. 5.3, б). Нас будет интересовать случайный интервал времени Т между соседними событиями в этом потоке; найдем его закон распределения. Сначала найдем функцию распределения:
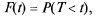
т. е. вероятность того, что величина Т будет иметь значение, меньшее, чем t. Отложим от начала интервала Т (точки 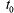 ) отрезок t и найдем вероятность того, что интервал Т будет меньше t. Для этого нужно, чтобы на участок длины t, примыкающий к точке
) отрезок t и найдем вероятность того, что интервал Т будет меньше t. Для этого нужно, чтобы на участок длины t, примыкающий к точке 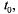 попало хотя бы одно событие потока. Вычислим вероятность этого F(t) через вероятность противоположного события (на участок t не попадет ни одного события потока):
попало хотя бы одно событие потока. Вычислим вероятность этого F(t) через вероятность противоположного события (на участок t не попадет ни одного события потока):
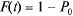
Вероятность 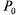 найдем по формуле (5.15), полагая m = 0:
найдем по формуле (5.15), полагая m = 0:
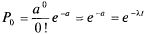
откуда функция распределения величины Т будет:
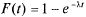 (5.16)
(5.16)
Чтобы найти плотность распределения 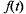 случайной величины Т, необходимо продифференцировать выражение (5.16) по t:
случайной величины Т, необходимо продифференцировать выражение (5.16) по t:
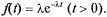 (5.17)
(5.17)
Закон распределения с плотностью (5.17) называется показательным (или экспоненциальным). Величина 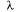 называется параметром показательного закона.
называется параметром показательного закона.
Показательный закон распределения играет большую роль в теории марковских случайных процессов.
Найдем числовые характеристики случайной величины Т — математическое ожидание (среднее значение) 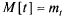 и дисперсию
и дисперсию  .
.
Имеем (интегрируя по частям):
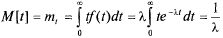 (5.18)
(5.18)
Дисперсия величины T составляет:
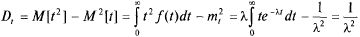 . (5.19)
. (5.19)
Извлекая корень квадратный из дисперсии, найдем среднее квадратическое отклонение случайной величины Т.
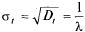 (5.20)
(5.20)
Итак, для показательного распределения математическое ожидание и среднее квадратическое отклонение равны друг другу и обратны параметру 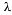 , где
, где 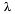 — интенсивность потока.
— интенсивность потока.
Приведем выражение для так называемого «элемента вероятности появления события» или вероятности наступления на элементарном участке 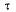 (рис 5.3, а) события потока.
(рис 5.3, а) события потока.
Найдем вероятность того, что на участке 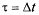 появится какое-то событие потока, т. е. участок не будет «пуст». Так как поток ординарен, вероятностью появления на участке более чем одного события можно пренебречь. Обозначим
появится какое-то событие потока, т. е. участок не будет «пуст». Так как поток ординарен, вероятностью появления на участке более чем одного события можно пренебречь. Обозначим 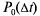 вероятность того, что на участке
вероятность того, что на участке 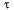 не будет события, а
не будет события, а 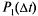 — вероятность того, что на нем появится одно событие.
— вероятность того, что на нем появится одно событие.
В силу ординарности потока
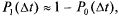
а вероятность 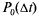 определяется по (5.15):
определяется по (5.15):
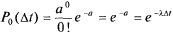
откуда
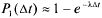
Разлагая 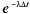 в ряд и пренебрегая величинами высшего порядка малости, получаем:
в ряд и пренебрегая величинами высшего порядка малости, получаем:
 (5.21)
(5.21)
Эта вероятность и называется «элементом вероятности появления события».
Очевидно, такая же формула будет справедлива и для нестационарного пуассоновского потока с той разницей, что величину 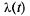 нужно брать равной ее значению в той точке t, к которой примыкает участок
нужно брать равной ее значению в той точке t, к которой примыкает участок 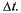
 2014-10-30
2014-10-30 425
425







