При наличии сопротивления трения

Рассмотрим адиабатическое, но неизэнтропическое движение газа по трубе постоянного сечения при наличии сопротивления трения. Для поддержания равномерного движения реальной жидкости в трубе постоянного сечения необходимо к сечениям трубы, ограничивающим участок длиной , приложить движущий перепад давления 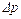, который смог бы уравновесить сопротивление трения, препятствующего движению жидкости по трубе. Этот переход давления выразится формулой, выведенной в курсе гидравлики

, (2.34)

где d – диаметр трубы; r – плотность жидкости, принимаемая постоянной; V _ср – средняя по сечению трубы скорость движения жидкости; l _тр – коэффициент сопротивления трения.

При принятом в данном курсе приближенном одномерном представлении движения будем считать среднюю скорость V _ср совпадающей со скоростью V одномерного движения, а коэффициент сопротивления трения l _тр – постоянной величиной, т.к. при больших скоростях он слабо зависит от Re, а сам критерий Рейнольдса на данном участке трубы меняется незначительно.

Применим формулу сопротивления (2.34) к сжимаемому газу на участке длиной

Применим уравнение Эйлера в дифференциальной форме для одномерного стационарного движения реального газа (для идеального газа оно имеет вид ). Для учета трения введем дополнительный перепад давления dp _тр. В результате получим

Представим это уравнение в виде

, (2.35)

где – удельная работа сил трения.

Используя дифференциальные формы уравнений неразрывности () и состояния () получим

. (2.36)

Подставим значение из (2.35) в (2.36) и после преобразования получим

С помощью выражения придадим уравнению следующий вид

. (2.37)

Так как (процесс энергетически изолированный), это эквивалентно условию

Отсюда

или

. (2.38)

Подставляя (2.38) в (2.37), приходим к соотношению, связывающему изменение скорости вдоль трубы постоянного сечения с работой сил трения:

. (2.39)

Трение является односторонним воздействием: работа сил трения всегда положительна (). Поэтому согласно (2.39) под влиянием трения дозвуковой поток (М < 1) ускоряется (dV > 0), а сверхзвуковой (M > 1) замедляется (dV < 0). Непрерывный переход через скорость звука при воздействии только трением невозможен.

Выведем формулы, определяющие изменение параметров газа вдоль изолированной трубы при наличии трения.

Так как температура торможения не меняется, т.е.

то термодинамическая температура определяется ранее полученными формулами

. (2.40)

Вследствие постоянства температуры торможения критическая скорость вдоль трубы также не изменяется; отсюда отношение скоростных коэффициентов равно отношению скоростей и на основании уравнений неразрывности – обратному отношению плотностей

. (2.41)

Подставив (2.40) и (2.41) в уравнение состояния, получим зависимость давления от приведенной скорости

, (2.42)

В виду постоянства температуры торможения полное давление пропорционально плотности заторможенного газа

Отсюда на основании (2.42) получим

. (2.43)

Присвоим 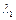какое-либо постоянное значение, и будем рассматривать как переменную величину, а параметры , , 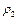, , 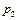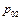– как функции переменной .

Трение ускоряет дозвуковой поток, что приводит к росту , и замедляет сверхзвуковой, вызывая уменьшение этой величины. Поэтому согласно (2.40), (2.41), (2.42) термодинамическая температура, плотность и статическое давление вдоль изолированной трубы под влиянием трения падают в дозвуковом потоке и растут в сверхзвуковом.

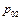Из (2.43) следует, что в критическом сечении при полное давление имеет минимальное значение. Согласно ранее приведенным выражениям энтропия в критическом сечении достигает максимального значения. Полное давление и плотность заторможенного газа в соответствии с (2.43) как в дозвуковом, так и в сверхзвуковом потоке вдоль трубы убывают, и только один параметр – температура торможения – не меняется.

На рисунке изображены кривые 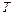, , 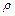, , 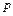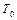в функции скоростного коэффициента для дозвукового потока (), и для сверхзвукового потока () при 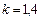. Стрелки на кривых указывают направление протекания процесса. Подчеркнем что значительное ускорение дозвукового и торможение сверхзвукового потоков под действием силы трения сопряжено с существенным расходованием полного давления.

Из рисунка видно, что в дозвуковом потоке при наличии трения скорость увеличивается, наиболее интенсивно падают статическое давление, плотность и полное давление, тогда как уменьшение температуры происходит в меньшей степени.

В сверхзвуковом потоке скорость падает, интенсивно падает полное давление, все остальные параметры растут в последовательности: статическое давление, температура и плотность.

Исследуем влияние трения на изменение скоростного коэффициента турбулентного газового потока в трубах постоянного диаметра. Работа силы трения записана ранее выражением

Подставив в формулу (2.39) получим

. (2.44)

Воспользовавшись постоянством критической скорости в трубе, из которого следует равенство

и формулой

перейдем в соотношении (2.44) от М к скоростному коэффициенту :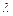

. (2.45)

Предположим, что коэффициент трения , как при дозвуковых, так и сверхзвуковых течениях газа в трубах не зависит от и .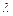

В шероховатых трубах для несжимаемой жидкости не зависит также от Re и определяется, например, по формуле

где – относительная шероховатость трубы (h – высота выступов шероховатости).

В технически гладких трубах для турбулентного потока несжимаемой жидкости коэффициент трения зависит от и определяется формулой

где .

Поскольку в трубе постоянного поперечного сечения согласно уравнению неразрывности , то по длине трубы изменяются незначительно (только за счет изменения коэффициента динамической вязкости m).

На основании вышесказанного полагаем в уравнении (2.45) и после интегрирования получим

. (2.46)

Здесь l ₁ – значение приведенной скорости в начале трубы при х = 0; l ₂ – значение приведенной скорости в сечении х = х ₂ от начала.

По уравнению (2.46) можно определить значение скоростного коэффициента в произвольном сечении трубы x, если известно l ₁, d, и k.

Введем функцию и назовем безразмерную величину, находящуюся в правой части уравнения (2.46) приведенной длиной трубы

, (2.47)

Тогда уравнение (2.46) можно представить в следующем виде

. (2.48)

Таким образом, изменение скорости потока между двумя сечениями трубы таково, что разность функций в них равна приведенной длине данного участка трубы. Пользуясь графиком функции , можно определить изменение скоростного коэффициента потока по длине трубы в зависимости от значения 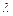и .

Функция имеет минимум, равный единице, при . Вследствие этого при заданном значении 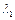величина разности в левой части уравнения (2.48), будет наибольшей при . Этому наибольшему значению соответствует некоторая критическая величина приведенной длины трубы .

. (2.49)

Действительно, приравняем нулю производную приведенной длины по при :

Отсюда находим

Так как при

то условие определяет максимум величины приведенной длины трубы для заданного значения скоростного коэффициента на входе в трубу .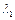

Поскольку уравнение (2.48) справедливо для любого участка трубы, то из него следует, что скорость, равная скорости звука, может быть достигнута только в выходном сечении трубы.

Действительно, если представить, что скоростной коэффициент 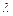равен единице в каком-либо промежуточном сечении цилиндрической трубы, то из уравнения (2.47), записанного для последующего участка трубы, получится

Так как по определению функция , (см. рис.) то этот случай нереален.

По уравнению (2.48) если на входе в трубу поток дозвуковой и его скоростной коэффициент равен 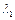и если приведенная длина трубы меньше критического значения, определяемого формулой (2.49), то на выходе из трубы поток будет также дозвуковым. Причем из (2.48) следует, что > .

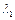Если поток на входе дозвуковой и приведенная длина трубы равна критической (максимальной) величине для данного 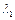, то на выходе из трубы скорость потока равна скорости звука и .

Если, наконец, приведенная длина трубы больше максимальной, определяемой из формулы (2.49), то уравнение (2.48) не имеет решения для l ₂ . Это означает, что принятое начальное значение приведенной скорости 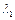не может быть реализовано. В начале трубы с заданной приведенной длиной скорость потока не может превышать величины, получаемой из формулы

так как при этом на выходе из трубы скорость равна критической, и через трубу протекает максимально возможный секундный расход газа.

На рисунке представлена зависимость предельного значения приведенной скорости на входе в трубу от безразмерной длины трубы х / d для дозвукового потока при и 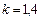. При этих значениях и

Следует отметить, что полученному изменению приведенной скорости [формула (2.46)] как при , так и при соответствует вполне определенное изменение полного и статического давления газа. Выше мы везде полагали, что такое изменение давления может быть всегда осуществлено (это являлось условием сохранения постоянного значения 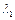при изменении приведенной длины трубы вплоть до получения ). Если почему-либо указанное изменение давления невозможно, например, при определенной величине перепада давлений в трубе, то рассматриваемое течение с заданной начальной приведенной скоростью может оказаться нереальным.

При сверхзвуковом течении, для которого формула (2.46) также пригодна, возможны следующие режимы:

× если при заданной начальной скорости 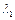приведенная длина меньше максимальной (), то в конце трубы получается сверхзвуковое течение ();

× если приведенная длина равна максимальной (), то в конце трубы скорость равна критической ();

× если же приведенная длина, вычисленная по формуле (2.47), получается больше максимальной, определенной по формуле (2.48) при заданном значении скоростного коэффициента в начале трубы 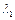, то плавное торможение сверхзвукового потока на протяжении всей трубы невозможно. В некотором сечении трубы произойдет скачок уплотнения, за которым установится ускоренное дозвуковое течение.

Определение положения этого скачка уплотнения можно произвести следующим образом.

Пусть задана сверхзвуковая скорость в начале трубы 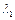, длина трубы х, диаметр трубы d, коэффициент трения и показатель адиабаты k. Вычисляем приведенную длину трубы по (2.47). По формуле (2.49) определяем и убеждаемся, что истинная приведенная длина больше максимальной (). То есть в некотором сечении, отстоящем на расстоянии от начала трубы, возникнет скачок уплотнения. Предполагаем скачек прямым, следовательно

где – скоростной коэффициент до скачка; – скоростной коэффициент после скачка.

Скоростной коэффициент перед скачком определяем из формулы (2.46)

. (2.50)

Скоростной коэффициент за скачком, где устанавливается ускоренное дозвуковое течение (), связан с длиной дозвукового участка трубы, в конце которого имеет место кризис (), формулой (2.48)

откуда

. (2.51)

Решая совместно два уравнения (2.50), (2.51) с двумя неизвестными (), приходим к уравнению с одним неизвестным, по которому вычисляем скорость перед скачком:

, (2.52)

после чего по формуле (2.51) определяем местоположение скачка.

Формулы (2.47) и (2.48) для определения местоположения скачка уплотнения неудобны, так как по ним приходится вести расчеты методом последовательных приближений. Поэтому применяют вспомогательные графики, существенно упрощающие расчеты.

Кривая 1 отвечает вспомогательной зависимости

. (2.53)

Кривая 2 изображает функцию (2.51)

Кривая 3 соответствует функции (2.48)

Поясним способ пользования этими кривыми на конкретном примере. Пусть дана труба с приведенной длиной . По кривой 3 видно, что в этой трубе установится критический режим () при значении приведенной скорости на входе . Проверим сначала характер течения в трубе в случае , например для . По формуле (2.46) можно вычислить скорость в конце трубы

или в соответствии с обозначением (2.53)

(2.54)

На кривой 1 по значению находим точку, у которой . Рассчитываем , и с помощью кривой 1 определяем значение приведенной скорости в конце трубы . Итак, в трубе, имеющей приведенную длину , при начальном значении приведенной скорости l ₁ = 2,2 происходит плавное торможение сверхзвукового потока до значения приведенной скорости l₂ = 1,4.

Пусть теперь труба имеет приведенную длину больше максимальной (). Данной задаче соответствуют значения l ₁ < 1,95. Положим l ₁ = 1,8. Тогда, согласно кривой 3, , т.е. .

В этом случае в трубе возникает скачок уплотнения, в результате чего на участке трубы длиной установится дозвуковое течение, причем, как видно из сравнения кривых 2 и 3, критическая длина трубы существенно увеличивается. Для отыскания местоположения скачка уплотнения преобразуем формулу (2.50) с помощью обозначений (2.53). Тогда расстояние от начала трубы до сечения, в котором происходит скачок уплотнения, равно

. (2.55)

Но, с другой стороны,

Заменяя последнее слагаемое в правой части этой формулы по (2.55), получаем

. (2.56)

Теперь, пользуясьграфиком, определим местоположение скачка уплотнения в трубе при l ₁ = 1,8. По кривой 1 находим j ₁ = 1,48, откуда .

Остается найти значение l ', при котором расстояние между кривыми 1 и 2 равно согласно (2.56) .

Из графика находим, что этой величине соответствуют значения .

Наконец, по формуле (2.54) определим приведенное расстояние от начала трубы до скачка уплотнения:

Описанным способом вычислены и нанесены на рисунок, расположенный справа, кривые изменения скоростного коэффициента в трубе с приведенной длиной = 0,6, получающиеся при различных значениях приведенной скорости l ₁ в начале трубы (при =0). Как видим, скачок уплотнения располагается тем ближе к началу трубы, чем меньше начальная сверхзвуковая скорость газа. Значения дозвуковой скорости после скачка уплотнения лежат во всех случаях на универсальной кривой, соответствующей формуле