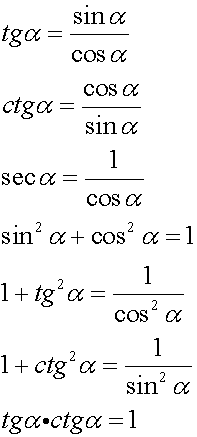
2)Понятие функции
Зависимость одной переменной от другой называется функциональной зависимостью. Зависимость переменной y от переменной x называется функцией, если каждому значению x соответствует единственное значение y.
Обозначение: 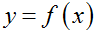
Переменную x называют независимой переменной или аргументом, а переменную y - зависимой. Говорят, что y является функцией от x. Значение y, соответствующее заданному значению x, называют значением функции.
Все значения, которые принимает x, образуют область определения функции; все значения, которые принимает y, образуют множество значений функции.
Обозначения: 
D(f) - значения аргумента. E(f) - значения функции. Если функция задана формулой, то считают, что область определения состоит из всех значений переменной, при которых эта формула имеет смысл.
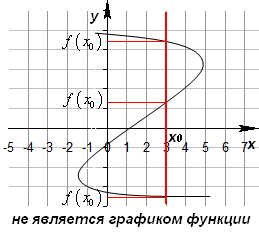
Графиком функции называется множество всех точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции. Если некоторому значению x=x0 соответствуют несколько значений (а не одно) y, то такое соответствие не является функцией. Для того чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая параллельная оси Оу, пересекалась с графиком не более чем в одной точке.
|
|
|

Способы задания функции
1) Функция может быть задана аналитически в виде формулы. Например, 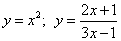
2) Функция может быть задана таблицей из множества пар (x; y).
3) Функция может быть задана графически. Пары значений (x; y) изображаются на координатной плоскости.
Монотонность функции
Функция f(x) называется возрастающей на данном числовом промежутке, если большему значению аргумента соответствует большее значение функции. Представьте, что некоторая точка движется по графику слева направо. Тогда точка будет как бы "взбираться" вверх по графику.
Функция f(x) называется убывающей на данном числовом промежутке, если большему значению аргумента соответствует меньшее значение функции. Представьте, что некоторая точка движется по графику слева направо. Тогда точка будет как бы "скатываться" вниз по графику.
Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.
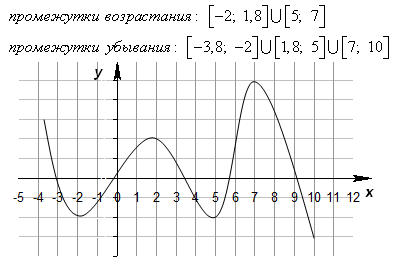
Нули функции и промежутки знакопостоянства
Значения х, при которых y=0, называется нулями функции. Это абсциссы точек пересечения графика функции с осью Ох.
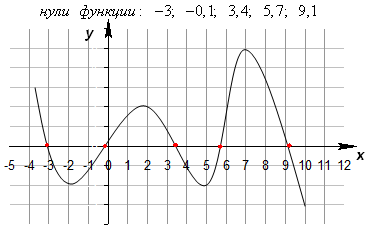
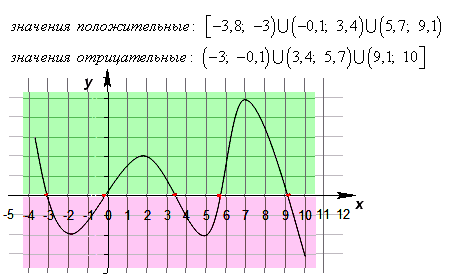
Такие промежутки значений x, на которых значения функции y либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.
|
|
|
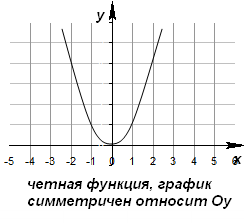
Четные и нечетные функции
Четная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
2) Для любого значения x, принадлежащего области определения, выполняется равенство f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.
Нечетная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
2) для любого значения x, принадлежащего области определения, выполняется равенство f(-x)=-f(x)
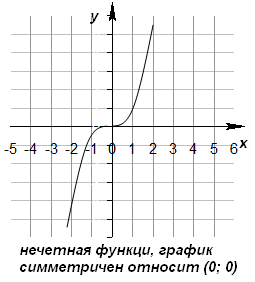
3) График нечетной функции симметричен относительно начала координат (0; 0).
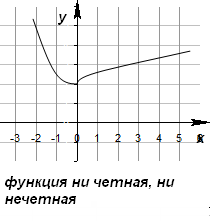
Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.
3) Исследование функции на монотонность
Функцию y=f(x) называют возрастающей на множестве X⊂D(f), если для любых точек x1 и x2 множества X таких, что x1<x2 выполняется неравенство f(x1)<f(x2).
Функцию y=f(x) называют убывающей на множестве X⊂D(f), если для любых точек x1 и x2 множества X таких, что x1<x2 выполняется неравенство f(x1)>f(x2).
Обрати внимание!
Иными словами:
функция возрастает, если большему значению аргумента соответствует большее значение функции;
функция убывает, если большему значению аргумента соответствует меньшее значение функции.
Исследование функции на ограниченность
Функцию y=f(x) называют ограниченной снизу на множестве X⊂D(f), если все значения этой функции на множестве X больше некоторого числа; иными словами, если существует число m такое, что для любого значения x∈X выполняется неравенство f(x)>m.
Функцию y=f(x) называют ограниченной сверху на множестве X⊂D(f), если все значения этой функции на множестве X меньше некоторого числа; иными словами, если существует число M такое, что для любого значения x∈X выполняется неравенство f(x)<M.
Наименьшее и наибольшее значения функции
Число m называют наименьшим значением функции y=f(x) на множестве X⊂D(f), если
1) существует точка x0∈X, такая что f(x0)=m;
2) для любого значения x∈X выполняется неравенство f(x)≥f(x0).
Число M называют наибольшим значением функции y=f(x) на множестве X⊂D(f), если
1) существует точка x0∈X, такая что f(x0)=M;
2) для любого значения x∈X выполняется неравенство f(x)≤f(x0).
Обозначения
yнаим наименьшее значение функции
yнаиб наибольшее значение функции
1) Если у функции существует yнаим, то она ограничена снизу.
2) Если у функции существует yнаиб, то она ограничена сверху.
3) Если функция не ограничена снизу, то у неё не существует yнаим.
4) Если функция не ограничена сверху, то у неё не существует yнаиб.
Нули функции
Нулём функции y=f(x) называется такое значение аргумента x0, при котором функция обращается в нуль.
4) Числовые последовательности. Способы задания и операции
Понятие числовой последовательности. Одним из основных понятий математики является натуральный ряд чисел  :
:  .Если каждому числу
.Если каждому числу 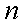 из натурального ряда чисел поставлено в соответствие вещественное число
из натурального ряда чисел поставлено в соответствие вещественное число 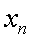 , то множество вещественных чисел
, то множество вещественных чисел 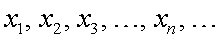 называется числовой последовательностью
называется числовой последовательностью  или просто последовательностью
или просто последовательностью  .Числа
.Числа 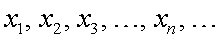 называются элементами (или членами) последовательности
называются элементами (или членами) последовательности  . Символ
. Символ 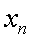 — общий элемент (член) последовательности, а
— общий элемент (член) последовательности, а 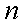 — его номер. Сокращенно последовательность обозначается символом
— его номер. Сокращенно последовательность обозначается символом 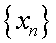 , а когда из контекста ясно, что речь идет о последовательности, то и просто символом
, а когда из контекста ясно, что речь идет о последовательности, то и просто символом 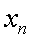 .
.
Пример 1. 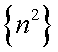 означает последовательность
означает последовательность 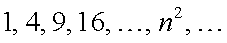 .
.
Пример 2.Дана формула общего элемента 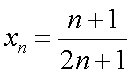 . Найти 5 первых элементов последовательности. Первые 5 элементов последовательности имеют вид:
. Найти 5 первых элементов последовательности. Первые 5 элементов последовательности имеют вид: 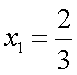 ;
;  ;
; 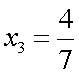 ;
; 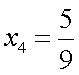 ;
; 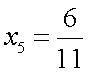 . Пример 3.Зная несколько первых элементов последовательности
. Пример 3.Зная несколько первых элементов последовательности 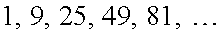 , написать формулу общего элемента. Видно, что каждый элемент последовательности представляет собой квадрат нечетного числа:
, написать формулу общего элемента. Видно, что каждый элемент последовательности представляет собой квадрат нечетного числа: 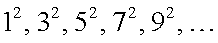 . Последовательность нечетных чисел есть
. Последовательность нечетных чисел есть 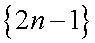 . Следовательно, формула общего элемента искомой последовательности может быть представлена в виде:
. Следовательно, формула общего элемента искомой последовательности может быть представлена в виде: 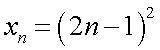 .Заметим, что знание нескольких первых элементов последовательности еще не определяет саму последовательность. Поэтому задачу отыскания формулы общего элемента последовательности по ее первым элементам необходимо рассматривать как задачу отыскания простой закономерности.Кроме того, вид формулы для
.Заметим, что знание нескольких первых элементов последовательности еще не определяет саму последовательность. Поэтому задачу отыскания формулы общего элемента последовательности по ее первым элементам необходимо рассматривать как задачу отыскания простой закономерности.Кроме того, вид формулы для 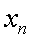 , определяемый по первым элементам последовательности, не является единственным. Например, последовательность
, определяемый по первым элементам последовательности, не является единственным. Например, последовательность 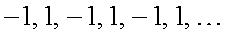 можно представить в различном виде:
можно представить в различном виде: 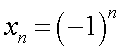 ;
; 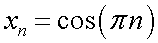 ;
; 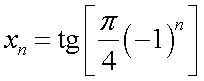 . Способы задания последовательности Последовательность может быть задана как с помощью формулы общего элемента
. Способы задания последовательности Последовательность может быть задана как с помощью формулы общего элемента 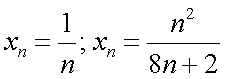 и т.д., так и с помощью рекуррентных соотношений
и т.д., так и с помощью рекуррентных соотношений  , когда задаются первый элемент (несколько первых элементов) последовательности
, когда задаются первый элемент (несколько первых элементов) последовательности  и формула, определяющая следующий элемент через предыдущий (несколько предыдущих). Пример 4 (арифметическая прогрессия). Арифметической прогрессией
и формула, определяющая следующий элемент через предыдущий (несколько предыдущих). Пример 4 (арифметическая прогрессия). Арифметической прогрессией  называется последовательность чисел, в которой следующее число есть предыдущее, увеличенное (уменьшенное) на постоянное число. В соответствии с определением, задается
называется последовательность чисел, в которой следующее число есть предыдущее, увеличенное (уменьшенное) на постоянное число. В соответствии с определением, задается 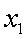 и рекуррентное соотношение
и рекуррентное соотношение 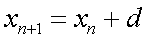 , где
, где 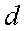 — разность арифметической прогрессии. Для арифметической прогрессии справедливы хорошо известные соотношения для формулы
— разность арифметической прогрессии. Для арифметической прогрессии справедливы хорошо известные соотношения для формулы 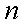 -го элемента
-го элемента 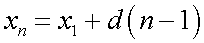 и для суммы первых
и для суммы первых 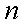 элементов
элементов 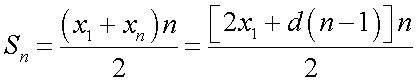 . Пример 5 (геометрическая прогрессия). Геометрической прогрессией
. Пример 5 (геометрическая прогрессия). Геометрической прогрессией  называется последовательность чисел, в которой следующее число есть предыдущее, умноженное на постоянное число. В соответствии с определением задается
называется последовательность чисел, в которой следующее число есть предыдущее, умноженное на постоянное число. В соответствии с определением задается 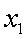 и рекуррентное соотношение
и рекуррентное соотношение 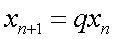 , где
, где 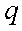 — знаменатель геометрической прогрессии. Для геометрической прогрессии также легко найти формулу для
— знаменатель геометрической прогрессии. Для геометрической прогрессии также легко найти формулу для 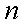 -го элемента
-го элемента 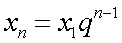 и сумму первых
и сумму первых 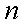 членов
членов 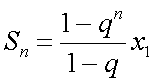 . Пример 6 (числа Фибоначчи). Задаются первые два элемента
. Пример 6 (числа Фибоначчи). Задаются первые два элемента 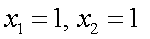 и рекуррентное соотношение
и рекуррентное соотношение 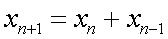 . Явный вид последовательности следующий:
. Явный вид последовательности следующий: 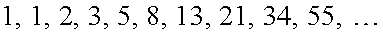 Операции над числовыми последовательностями Произведением последовательности
Операции над числовыми последовательностями Произведением последовательности 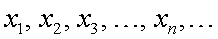 на число
на число 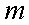
 называется последовательность
называется последовательность 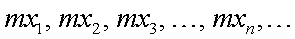 . Суммой последовательностей
. Суммой последовательностей 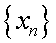 и
и 
 называется последовательность
называется последовательность 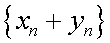 , т.е.
, т.е. 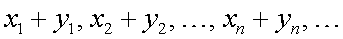 (к
(к 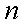 -му элементу первой последовательности прибавляется
-му элементу первой последовательности прибавляется 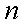 -й элемент второй последовательности и получившаяся сумма есть
-й элемент второй последовательности и получившаяся сумма есть 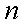 -й элемент новой последовательности). Или сокращенно
-й элемент новой последовательности). Или сокращенно 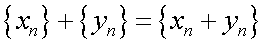 . Разностью последовательностей
. Разностью последовательностей 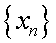 и
и 
 называется последовательность
называется последовательность 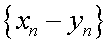 . Произведением последовательностей
. Произведением последовательностей 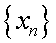 и
и 
 называется последовательность
называется последовательность  . Частным последовательностей
. Частным последовательностей 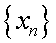 и
и 
 называется последовательность
называется последовательность 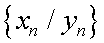 , причем
, причем 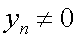
|
|
|
|
|
|
 2015-01-30
2015-01-30 2766
2766








