Основной задачей корреляционного анализа является выявление связи между случайными переменными и оценка её тесноты.
Рассмотрим две случайные величины 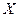 ,
,  и наиболее важный для практики случай, когда они связаны линейной зависимостью
и наиболее важный для практики случай, когда они связаны линейной зависимостью
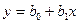 .
.
Тогда показателем тесноты линейной связи является выборочный коэффициент корреляции
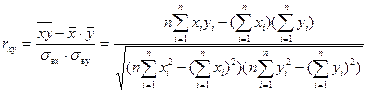 . (22)
. (22)
Коэффициент 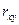 является точечной оценкой неизвестного коэффициента корреляции
является точечной оценкой неизвестного коэффициента корреляции 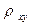 , который существует в природе.
, который существует в природе.
Основные свойства 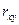 :
:
1. Значения 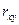 изменяются в пределах:
изменяются в пределах: 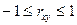 . Если
. Если 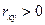 , то говорят о прямой связи переменных
, то говорят о прямой связи переменных 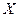 и
и  , в противном случае (
, в противном случае (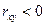 ) – об обратной.
) – об обратной.
2. Если 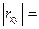 1, то корреляционная связь представляет линейную функциональную зависимость.
1, то корреляционная связь представляет линейную функциональную зависимость.
3. Если 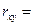 0, то линейная корреляционная связь отсутствует.
0, то линейная корреляционная связь отсутствует.
Характеристику связи при других значениях коэффициента 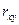 даёт шкала Чеддока:
даёт шкала Чеддока:
Значения 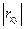
| 0,1 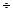 0.3 0.3
| 0,3 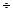 0,5 0,5
| 0,5 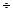 0,7 0,7
| 0,7 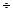 0,9 0,9
| 0,9 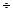 0,99 0,99
|
| Характеристика связи | слабая | умеренная | заметная | высокая | весьма высокая |
Для оценки значимости 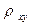 тестируется гипотеза
тестируется гипотеза
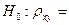 0 при альтернативной
0 при альтернативной 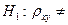 0.
0.
|
|
|
Гипотеза проверяется с использованием статистического критерия
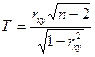 , (23)
, (23)
который при справедливости гипотезы 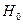 имеет распределение Стьюдента с
имеет распределение Стьюдента с 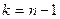 степенями свободы.
степенями свободы.
По формуле (23) находится значение 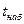 и если |
и если | 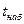 |
| 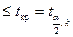 , то гипотеза
, то гипотеза 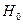 принимается на уровне значимости
принимается на уровне значимости 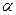 . В противном случае – отвергается.
. В противном случае – отвергается.
Если 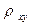 является статистически значимым, то для него можно построить доверительный интервал. Для этого используют
является статистически значимым, то для него можно построить доверительный интервал. Для этого используют 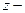 преобразование Фишера:
преобразование Фишера:
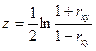 . (24)
. (24)
Вначале строят доверительный интервал для математического ожидания 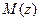 переменной
переменной 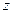
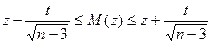 , (25)
, (25)
где 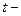 значение аргумента функции Лапласа, находимое из равенства
значение аргумента функции Лапласа, находимое из равенства
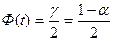 . (26)
. (26)
Далее уже строят доверительный интервал для 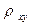 :
:
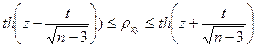 .
.
Значения гиперболического тангенса 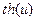 находят, либо, используя его формулу
находят, либо, используя его формулу
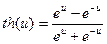 ,
,
либо из специальных таблиц для гиперболического тангенса.
Пример 18. Имеются данные о производительности труда  (тыс. руб) и энерговооруженности труда
(тыс. руб) и энерговооруженности труда  (кВт) в расчете на одного работающего для 14 предприятий региона (табл.14).
(кВт) в расчете на одного работающего для 14 предприятий региона (табл.14).
Таблица 14
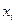
| 2,8 | 2,2 | 3,0 | 3,5 | 3,2 | 3,7 | 4,0 | 4,8 | 6,0 | 5,4 | 5,2 | 5,4 | 6,0 | 9,0 |
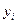
| 6,7 | 6,9 | 7,2 | 7,3 | 8,4 | 8,8 | 9,1 | 9,8 | 10,6 | 10,7 | 11,1 | 11,8 | 12,1 | 12,4 |
Требуется:
1. Оценить тесноту и направление связи между переменными с помощью коэффициента парной корреляции.
2. Проверить значимость коэффициента корреляции.
3. Построить для коэффициента корреляции 95% доверительный интервал.
Решение. 1. Вычислим выборочный коэффициент корреляции по формуле (22). Найдем для этого необходимые суммы:
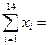 2,8+2,2+…+6,0+9,0=64,2;
2,8+2,2+…+6,0+9,0=64,2;
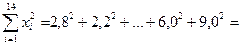 335,26;
335,26;
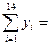 6,7+6,9+…+12,1+12,4=132,9;
6,7+6,9+…+12,1+12,4=132,9;
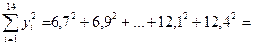 1313,95;
1313,95;
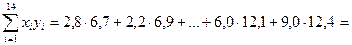 650,99.
650,99.
Подставляя полученные суммы в формулу (22), получим
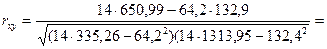 0,898.
0,898.
Таким образом, связь между переменными прямая и высокая по шкале Чеддока.
|
|
|
2. Проверим значимость коэффициента корреляции путём тестирования гипотезы 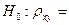 0 при альтернативной
0 при альтернативной 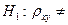 0.
0.
По формуле (23) вычисляем наблюдаемое значение критерия
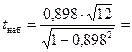 7,07.
7,07.
Из таблицы распределения Стьюдента (приложение 2) находим
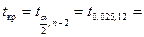 2,179.
2,179.
Поскольку 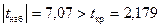 , то гипотеза
, то гипотеза 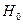 отвергается на уровне значимости
отвергается на уровне значимости 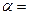 0,05 в пользу гипотезы
0,05 в пользу гипотезы 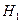 , т.е. коэффициент корреляции
, т.е. коэффициент корреляции 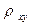 является статистически значимым (существенно отличается от нуля).
является статистически значимым (существенно отличается от нуля).
3. Так как коэффициент корреляции 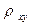 статистически значим, то для него можно построить доверительный интервал, применяя
статистически значим, то для него можно построить доверительный интервал, применяя 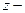 преобразование Фишера.
преобразование Фишера.
По формуле (24) определяем значение переменной 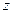 :
:
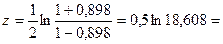 1,466.
1,466.
Поскольку 95% доверительный интервал соответствует доверительной вероятности 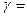 0,95, то
0,95, то 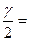 0,475 и из равенства (26) находим по таблицам функции Лапласа (приложение 1) значение аргумента
0,475 и из равенства (26) находим по таблицам функции Лапласа (приложение 1) значение аргумента 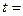 1,96.
1,96.
Вычислим 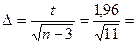 0,591.
0,591.
Далее по формуле (25) находим 95% доверительный интервал для 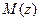 :
:
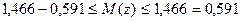
или
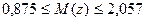 .
.
Отсюда доверительный интервал для 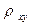 :
:
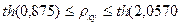 .
.
Воспользовавшись таблицами гиперболического тангенса (приложение 4), находим окончательно 95% доверительный интервал для коэффициента корреляции 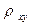 :
:
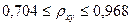 .
.
 2015-01-07
2015-01-07 1461
1461








