Пусть оценивается некоторый параметр 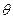 признака
признака 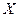 генеральной совокупности. Для этого извлечена выборка объёма
генеральной совокупности. Для этого извлечена выборка объёма 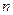 :
: 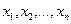 .
.
Точечной оценкой  параметра
параметра 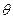 называют числовое значение некоторой подобранной функции, полученное по результатам выборки, т.е.
называют числовое значение некоторой подобранной функции, полученное по результатам выборки, т.е.
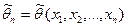 . (16)
. (16)
Оценка  зависит от значений
зависит от значений 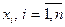 , поэтому является случайной величиной.
, поэтому является случайной величиной.
Для того чтобы точечная оценка давала хорошее приближение оцениваемого параметра, она должна быть: несмещенной, эффективной, состоятельной.
Оценка 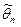 параметра
параметра 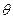 называется несмещённой, если её математическое ожидание равно самому оцениваемому параметру, т.е.
называется несмещённой, если её математическое ожидание равно самому оцениваемому параметру, т.е.
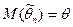 .
.
В противном случае оценку называют смещенной.
Несмещенная оценка 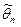 называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра
называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра 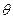 , вычисленных по выборке объёма
, вычисленных по выборке объёма 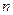 , т.е.
, т.е.
 .
.
Оценка 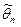 параметра
параметра 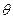 называется состоятельной, если при
называется состоятельной, если при 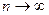 она сходится по вероятности к оцениваемому параметру, т.е.
она сходится по вероятности к оцениваемому параметру, т.е.
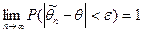 .
.
Доказано, что выборочное среднее
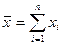 (16)
(16)
является несмещенной и состоятельной оценкой математического ожидания 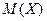 генеральной совокупности. Если
генеральной совокупности. Если 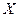 имеет нормальный закон распределения, то
имеет нормальный закон распределения, то 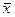 будет и эффективной оценкой.
будет и эффективной оценкой.
|
|
|
Выборочная дисперсия
 (17)
(17)
является смещённой и состоятельной оценкой дисперсии 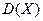 генеральной совокупности.
генеральной совокупности.
Чтобы получить несмещенную оценку 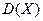 выборочную дисперсию
выборочную дисперсию 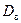 корректируют и вычисляют исправленную выборочную дисперсию
корректируют и вычисляют исправленную выборочную дисперсию
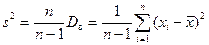 . (18)
. (18)
Исправленная дисперсия 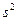 при
при 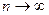 становится эффективной.
становится эффективной.
Несмещённой оценкой СКО  генеральной совокупности является исправленное СКО
генеральной совокупности является исправленное СКО
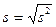 .
.
Интервальной оценкой параметра 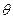 называют числовой интервал (
называют числовой интервал (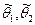 ), который с наперёд заданной вероятностью
), который с наперёд заданной вероятностью 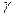 накрывает неизвестное значение параметра
накрывает неизвестное значение параметра 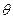 .
.
Сам интервал (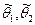 ) называют доверительным интервалом, а вероятность
) называют доверительным интервалом, а вероятность 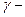 доверительной вероятностью.
доверительной вероятностью.
Пусть 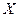 имеет нормальный закон распределения с неизвестным математическим ожиданием
имеет нормальный закон распределения с неизвестным математическим ожиданием  и неизвестной дисперсией
и неизвестной дисперсией 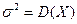 . По выборке объёма
. По выборке объёма 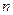 получены несмещённые оценки этих параметров:
получены несмещённые оценки этих параметров: 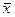 и
и 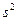 соответственно. Тогда интервальные оценки для
соответственно. Тогда интервальные оценки для 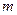 и СКО
и СКО 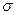 находятся по следующим формулам:
находятся по следующим формулам:
 , (19)
, (19)
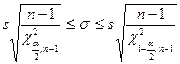 . (20)
. (20)
Здесь  критическая точка распределения Стьюдента находится из таблиц по двум входным данным: вероятности
критическая точка распределения Стьюдента находится из таблиц по двум входным данным: вероятности 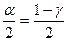 и числу степеней свободы
и числу степеней свободы 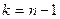 ;
; 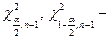 критические точки
критические точки  распределения также находятся из таблиц по заданному значению
распределения также находятся из таблиц по заданному значению  и числу степеней свободы
и числу степеней свободы 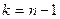 .
.
Статистической гипотезой называют любое предположение о виде закона распределения случайной величины, либо предположение о значениях параметров известных распределений.
Выдвинутую гипотезу называют нулевой и обозначают символом 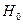 . Наряду с ней рассматривают альтернативную или конкурирующую гипотезу
. Наряду с ней рассматривают альтернативную или конкурирующую гипотезу 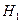 , которая противоречит
, которая противоречит 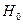 . Конкурирующих гипотез может быть несколько. Для проверки гипотезы
. Конкурирующих гипотез может быть несколько. Для проверки гипотезы 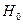 используют выборку. Если статистические данные противоречат
используют выборку. Если статистические данные противоречат 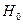 , то её отклоняют.
, то её отклоняют.
|
|
|
Для тестирования 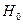 используется специально подобранная случайная величина
используется специально подобранная случайная величина 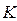 , называемая статистическим критерием (статистикой)
, называемая статистическим критерием (статистикой)
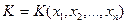 .
.
Подбор критерия осуществляется так, чтобы его закон распределения при справедливости 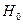 был либо точно, либо достаточно точно известен.
был либо точно, либо достаточно точно известен.
Множество возможных значений критерия 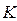 разбивается на два непересекающихся подмножества: область принятия гипотезы
разбивается на два непересекающихся подмножества: область принятия гипотезы 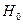 и критическую область, попадание в которую критерия
и критическую область, попадание в которую критерия 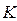 позволяет отвергнуть гипотезу
позволяет отвергнуть гипотезу 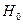 .
.
В зависимости от вида конкурирующей гипотезы 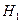 критическая область может быть трёх видов: двусторонняя, правосторонняя, левосторонняя.
критическая область может быть трёх видов: двусторонняя, правосторонняя, левосторонняя.
Точки, разделяющие эти два подмножества, называются критическими.
Критические точки выбирают так, чтобы вероятность попадания 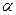 критерия
критерия 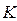 в критическую область была очень малой величиной.
в критическую область была очень малой величиной.
Значения 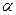 выбирают в диапазоне от 0,1 до 0,01 и называют уровнем значимости. Уровень значимости и доверительная вероятность
выбирают в диапазоне от 0,1 до 0,01 и называют уровнем значимости. Уровень значимости и доверительная вероятность 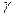 связаны соотношением
связаны соотношением  .
.
Рассмотрим схему проверки гипотезы о математическом ожидании. Пусть 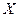 имеет нормальный закон распределения с неизвестным математическим ожиданием
имеет нормальный закон распределения с неизвестным математическим ожиданием 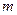 и неизвестной дисперсией
и неизвестной дисперсией 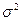 . Задан уровень значимости
. Задан уровень значимости 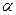 .
.
По выборке объёма 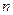 :
: 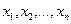 вычислено среднее выборочное
вычислено среднее выборочное 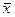 и исправленная выборочная дисперсия
и исправленная выборочная дисперсия 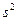 .
.
Выдвигается гипотеза
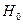 :
: 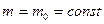 ,
,
которая тестируется с помощью критерия
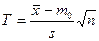 . (21)
. (21)
Доказано, что при выполнении гипотезы 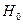 случайная величина
случайная величина 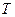 имеет распределение Стьюдента с
имеет распределение Стьюдента с 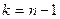 степенями свободы.
степенями свободы.
Если 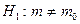 , то критическая область будет двусторонней симметричной относительно начала координат и её границы
, то критическая область будет двусторонней симметричной относительно начала координат и её границы
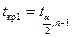 и
и 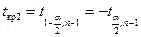
находятся по таблице распределения Стьюдента по заданному уровню значимости 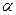 и числу степеней свободы
и числу степеней свободы 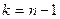 .
.
По формуле (21) вычисляется наблюдаемое значение статистического критерия  .
.
При выполнении неравенства 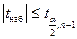 принимается гипотеза
принимается гипотеза 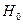 , в противном случае (
, в противном случае (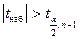 ) она отвергается в пользу альтернативной гипотезы
) она отвергается в пользу альтернативной гипотезы 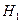 .
.
Пример 17. При оценке свойств картофеля было обследовано 10 проб и получены следующие значения содержания крахмала 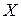 :
:
Таблица 11
| Содержание крахмала, % | |||||||||
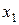
| 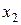
| 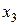
| 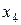
| 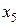
| 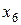
| 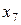
| 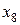
| 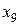
| 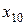
|
| 5,2 | 5,8 | 5,7 | 6,0 | 5,9 | 5,3 | 4,9 | 5,1 | 5,3 | 5,8 |
Требуется:
1. Определить выборочное среднее 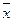 , выборочную дисперсию
, выборочную дисперсию 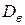 , выборочное среднее квадратическое отклонение
, выборочное среднее квадратическое отклонение 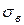 , исправленную дисперсию
, исправленную дисперсию 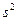 и среднее квадратическое отклонение
и среднее квадратическое отклонение 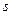 для величины
для величины 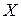 .
.
2. Полагая, что изменчивость величины 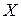 описывается законом нормального распределения, найти доверительные интервалы для ожидаемого среднего значения
описывается законом нормального распределения, найти доверительные интервалы для ожидаемого среднего значения 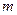 и ожидаемого среднего квадратического отклонения
и ожидаемого среднего квадратического отклонения 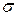 содержания крахмала с заданной надежностью
содержания крахмала с заданной надежностью 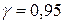 , а также вероятность того, что величина содержания крахмала
, а также вероятность того, что величина содержания крахмала 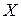 в выбранной наудачу пробе окажется в пределе от
в выбранной наудачу пробе окажется в пределе от 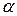 до
до 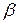 .
.
3. Проверить на уровне значимости  нулевую гипотезу
нулевую гипотезу 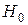 :
: 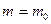 при конкурирующей гипотезе
при конкурирующей гипотезе 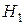 :
: 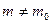 .
.
Задачу решить для следующих значений параметров 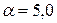 ,
,  ,
, 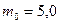 .
.
Решение. 1. Выборочное среднее при объеме выборки 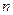 =10 находится по по формуле (16):
=10 находится по по формуле (16):
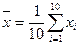 .
.
Подставляя в формулу значения  из таблицы 11, получим
из таблицы 11, получим
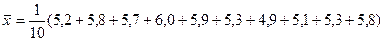 =5,5 (%).
=5,5 (%).
Для вычисления выборочной дисперсии используется формула (17) 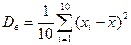 .
.

Составим следующую вспомогательную таблицу, куда внесем отклонения 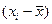 и их квадраты
и их квадраты 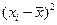 .
.
Таблица 12
| Содержание крахмала в пробе, % | 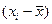
| 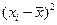
|
| 5,2 | -0,3 | 0,09 |
| 5,8 | 0,3 | 0,09 |
| 5,7 | 0,2 | 0,04 |
| 6,0 | 0,5 | 0,25 |
| 5,9 | 0,4 | 0,16 |
| 5,3 | -0,2 | 0,04 |
| 4,9 | -0,6 | 0,36 |
| 5,1 | -0,4 | 0,16 |
| 5,3 | -0,2 | 0,04 |
| 5,8 | 0,3 | 0,09 |
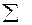
| - | 1,32 |
По данным таблицы 12 определим выборочное среднее
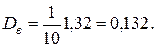
Далее вычисляем выборочное среднее квадратическое отклонение
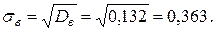
Исправленную дисперсию 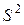 находим по формуле (18):
находим по формуле (18):
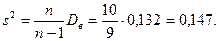
Исправленное стандартное отклонение 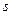 вычисляют путем извлечения квадратного корня из
вычисляют путем извлечения квадратного корня из 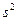 :
:
|
|
|

2. Доверительный интервал для математического ожидания 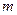 нормально распределенного признака
нормально распределенного признака 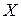 при неизвестных
при неизвестных 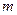 и
и 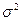 определяется по формуле (19).
определяется по формуле (19).
По заданной вероятности 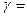 0,95 находим
0,95 находим  0,05 и
0,05 и 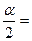 0,025. Так как
0,025. Так как 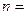 10, то число степеней свободы
10, то число степеней свободы 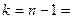 9. Отсюда по таблице распределения Стьюдента (приложение 2) находим
9. Отсюда по таблице распределения Стьюдента (приложение 2) находим
 2,262.
2,262.
Вычислим 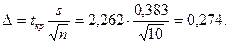
Тогда
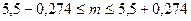
или
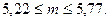
Интервальная оценка среднего квадратического отклонения 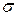 нормально распределенного количественного признака
нормально распределенного количественного признака 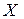 находится по формуле (20):
находится по формуле (20):
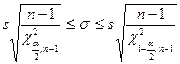 .
.
Найдем критические точки  . Величина
. Величина 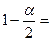 0,975, отсюда по таблице
0,975, отсюда по таблице  распределения (приложение 3) находим
распределения (приложение 3) находим
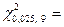 19,02;
19,02; 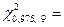 2,70.
2,70.
В итоге получаем

Чтобы найти вероятность того, что величина содержания крахмала 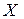 в выбранной наудачу пробе окажется в пределе от
в выбранной наудачу пробе окажется в пределе от 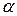 до
до 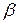 воспользуемся точечными несмещёнными оценками параметров нормального распределения
воспользуемся точечными несмещёнными оценками параметров нормального распределения 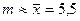 и
и 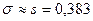 .
.
Воспользуемся известной формулой для подсчёта вероятности нахождения нормально распределённой случайной величины 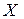 в заданном интервале через функцию Лапласа
в заданном интервале через функцию Лапласа 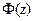 :
:
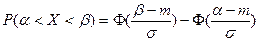 ,
,
в которой заменим 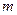 и
и 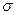 их оценками
их оценками 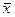 и
и 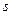 соответственно.
соответственно.
Учитывая нечетность функции Лапласа 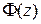 , с использованием таблиц функции Лапласа (приложение 1) получим
, с использованием таблиц функции Лапласа (приложение 1) получим
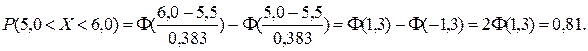
3. Для того чтобы при заданном уровне значимости 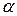 , проверить нулевую гипотезу
, проверить нулевую гипотезу 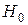 :
: 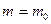 о равенстве неизвестной генеральной средней
о равенстве неизвестной генеральной средней 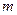 гипотетическому значению
гипотетическому значению 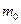 при конкурирующей гипотезе
при конкурирующей гипотезе 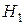 :
: 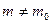 , надо по формуле (21) вычислить наблюдаемое значение статистического критерия
, надо по формуле (21) вычислить наблюдаемое значение статистического критерия  .
.
Найдем наблюдаемое значение критерия
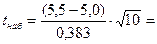 4,128.
4,128.
В таблице критических точек распределения Стьюдента (приложение 2) по заданному значению 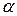 =0,05 и числу степеней свободы
=0,05 и числу степеней свободы 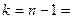 9 находим
9 находим
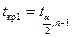 =
= 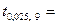 2,262.
2,262.
Так как выполняется неравенство 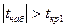 , то нулевая гипотеза
, то нулевая гипотеза 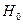 отвергается и выборочная средняя
отвергается и выборочная средняя 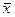 =5,5 значимо отличается от предполагаемого значения генеральной средней
=5,5 значимо отличается от предполагаемого значения генеральной средней 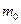 =5,0.
=5,0.
Заметим, что если бы проверялась нулевая гипотеза для 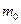 =5,3, то наблюдаемое значение критерия было бы
=5,3, то наблюдаемое значение критерия было бы 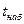 =1,65 и нулевую гипотезу не было бы оснований отвергать и
=1,65 и нулевую гипотезу не было бы оснований отвергать и 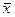 незначимо отличалась бы от
незначимо отличалась бы от 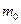 .
.
 2015-01-07
2015-01-07 1300
1300








