2015-01-21
1172
Пример 4.1. По статистическим данным таблицы 4.2:
1) на основании анализа матрицы парных коэффициентов корреляции из трех независимых переменных отобрать два наиболее существенных фактора;
2) для отобранных факторов построить двухфакторное уравнение линейной регрессии;
3) определить коэффициент множественной корреляции;
4) проверить значимость уравнения при уровнях значимости 0,05 и 0,01.
Таблица 4.2. Статистические данные примера 4.1
| 
| 
| 
| |
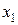
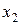
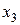
Решение:
|
|
|
1) Построим матрицу парных коэффициентов корреляции, используя функцию «Сервис. Анализ данных. Корреляция» табличного процессора MS Excel (таблица 4.3).
Таблица 4.3. Матрица парных коэффициентов корреляции примера 4.1
|
|
|
|
| |
|
| ||||
|
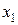
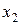
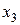
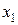
| 0, 638 | |||
|
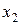
| 0,680 | 0,710 | ||
|
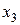
| 0,661 | 0,513 | 0,506 |
Из матрицы следует, что наблюдается явная коллинеарность между факторам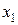и и 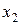, так как 
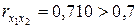. Для дальнейшего рассмотрения оставляем фактор 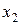, так как он меньше коррелирует с фактором (
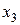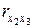= 0,506 < 
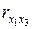= 0,513) и теснее связан с результативным фактором .
Таким образом, далее будет строиться регрессия переменной y на факторы 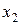и .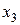
2) Для построения уравнения множественной линейной регрессии используем функцию «Сервис. Анализ данных. Регрессия». Задав соответствующие диапазоны данных, получим следующий набор таблиц А, Б, В.
Таблица А
| Показатель | Значение | Комментарии |
| Множественный R | 0,773 | Множественный коэффициент корреляции |
| R-квадрат | 0,597 | |
| Нормированный R-квадрат | 0,566 | |
| Стандартная ошибка | 7,768 | Стандартная ошибка регрессии |
| Наблюдения | Число наблюдений |
Таблица Б
| Число степеней свободы | Дисперсия | Дисперсия на 1 степень свободы | Статистика Фишера | ||
| df | SS | MS | F | Значимость F | |
| Регрессия | 2326,1 | 1163,1 | 19,3 | 7,35Е-06 | |
| Остаток | 1569,1 | 60,3 | |||
| Итого | 3895,2 |
Таблица В
| Коэффициенты уравнения регрессии | Стандартная ошибка определения коэффициентов | t- статистика | Вероятность ошибки | Нижние 95%-пределы | Верхние 95%-пределы | |
| Коэффициенты | Стандартная ошибка | t- статистика | P-значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 92,585 | 8,351 | 11,087 | 0,0000 | 75,420 | 109,750 |
| Переменная x2 | 1,761 | 0,547 | 3,219 | 0,0030 | 0,637 | 2,886 |
| Переменная x3 | 0, 397 | 0,134 | 2,952 | 0,0070 | 0,120 | 0,673 |
Из таблицы В следует, что уравнение регрессии имеет вид
|
|
|
.
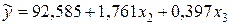3) Коэффициент множественной корреляции определяется из таблицы А: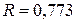 
.
4) Проверка значимости уравнения регрессии основана на использовании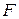 
-критерии Фишера. Фактическое значение критерия берется из таблицы Б: 
.
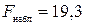Для определения табличных значений используем встроенную функцию MS Excel «FPAСПОБР», задавая параметры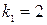 
, 
, 
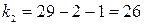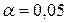и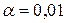 
.
В результате получаем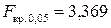 
, 
.
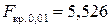Откуда следует, что уравнение регрессии значимо при 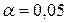и .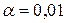
Пример 4.2. По статистическим данным, приведенным в таблице 4.4, построить линейную регрессионную модель зависимости заработной платы (доллары) рабочих некоторого предприятия от их возраста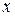 
(годы) и пола 
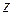(мужской или женский).
Таблица 4.4. Статистические данные примера 4.2
| Заработная плата,
| Возраст,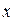 
| Пол,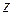
|
| ж | ||
| м | ||
| ж | ||
| ж | ||
| м | ||
| м | ||
| ж | ||
| м | ||
| м | ||
| м | ||
| ж | ||
| м | ||
| м | ||
| м | ||
| ж | ||
| м | ||
| м | ||
| м | ||
| ж | ||
| м |
Решение:
Переменная 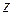является фиктивной:
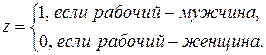
Модель будем строить в виде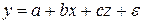 
. Параметризуя ее (например, с помощью табличного процессора MS Excel), найдем коэффициенты регрессии 
, 
, 
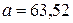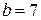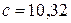. Поэтому уравнение регрессии имеет вид 
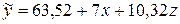. При этом 
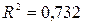и коэффициент детерминации значим (наблюдаемое значение 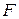-критерия больше критического). Правда, коэффициент регрессии при фиктивной переменной является незначимым (это может объясняться малым размером выборки).
Коэффициент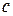 
в уравнении регрессии интерпретируется следующим образом: при одном и том же возрасте заработная плата мужчин-рабочих на 10,32 доллара выше, чем у женщин-рабочих.
Пример 4.3. Построить производственную функцию Кобба-Дугласа для оценки национального дохода США по статистическим данным, представленным в таблице 4.5: – национальный доход США, млрд. долл.,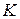 
– капиталовложения, млрд. долл., 
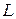– общее число занятых в экономике, тыс. чел. (источник данных: www.economagic.com).
Таблица 4.5. Статистические данные примера 4.3
| Год |
|
|
|
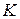
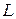
| 6337,75 | 5512,75 | ||
| 6657,4 | 5773,35 | ||
| 7072,23 | 6122,25 | ||
| 7397,65 | 6453,93 | ||
| 7816,83 | 6840,1 | ||
| 8304,33 | 7292,18 | ||
| 8746,98 | 7752,8 | ||
| 9268,43 | 8236,65 | ||
| 9816,98 | 8795,23 | ||
| 10100,83 | 9881,23 | ||
| 10480,83 | 9290,85 | ||
| 10985,45 | 9600,47 |
Решение:
Логарифмируя обе части уравнения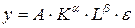 
, приходим к линейной модели 
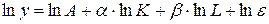. По статистическим данным таблицы 4.5 рассчитаем значения логарифмов. Результаты вычислений сведем в таблицу 4.6.
Таблица 4.6. Значения логарифмов
| 
| 
|
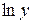
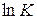
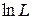
| 8,754279 | 8,614819 | 11,7002 |
| 8,803484 | 8,661008 | 11,71209 |
| 8,863931 | 8,719685 | 11,718 |
| 8,908918 | 8,772445 | 11,73496 |
| 8,964034 | 8,830558 | 11,74801 |
| 9,024532 | 8,894558 | 11,7703 |
| 9,076464 | 8,955809 | 11,7851 |
| 9,134369 | 9,016349 | 11,80049 |
| 9,191869 | 9,081965 | 11,82619 |
| 9,220373 | 9,198392 | 9,526172 |
| 9,257303 | 9,136785 | 11,71891 |
| 9,304327 | 9,169567 | 11,832 |
Параметризуя модель 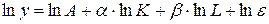по данным значений логарифмов таблицы 4.6 (например, с помощью табличного процессора MS Excel), найдем 
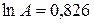(тогда 
), 
, 
.
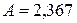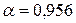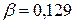Таким образом, производственная функция имеет вид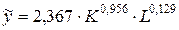 
. Это означает, что при увеличении капиталовложений на 1% национальный доход США увеличивается на 0,956%, а при увеличении численности занятых в экономике на 1% национальный доход увеличивается на 0,129%.
Пример 4.4. По 20 предприятиям региона (таблица 4.7) изучается зависимость выработки продукции на одного работника (млн руб.) от ввода в действие новых основных фондов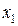 
(% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих 
(%).
|
|
|
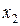Таблица 4.7. Статистические данные примера 4.4
| Номер предприятия |
|
|
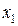
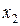
| Номер предприятия |
|
|
|
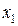
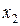
| 7,0 | 3,9 | 10,0 | 9,0 | 6,0 | 21,0 | ||
| 7,0 | 3,9 | 14,0 | 11,0 | 6,4 | 22,0 | ||
| 7,0 | 3,7 | 15,0 | 9,0 | 6,8 | 22,0 | ||
| 7,0 | 4,0 | 16,0 | 11,0 | 7,2 | 25,0 | ||
| 7,0 | 3,8 | 17,0 | 12,0 | 8,0 | 28,0 | ||
| 7,0 | 4,8 | 19,0 | 12,0 | 8,2 | 29,0 | ||
| 8,0 | 5,4 | 19,0 | 12,0 | 8,1 | 30,0 | ||
| 8,0 | 4,4 | 20,0 | 12,0 | 8,5 | 31,0 | ||
| 8,0 | 5,3 | 20,0 | 14,0 | 9,6 | 32,0 | ||
| 10,0 | 6,8 | 20,0 | 14,0 | 9,0 | 36,0 |
Требуется:
1) Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.
2) Найти коэффициенты парной и множественной корреляции. Проанализировать их. Обосновать включение обоих факторов в модель или исключение одного из факторов.
3) Вычислить коэффициент детерминации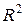 
. С помощью 
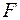-критерия Фишера оценить статистическую надежность уравнения множественной регрессии.
4) С помощью Стьюдента t- статистики оценить статистическую значимость коэффициентов линейной множественной регрессии.
Решение:
1) Вычислим параметры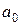 
, 
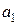и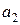 
линейного уравнения 
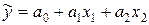множественной регрессии. Решая систему уравнений (4.3), получим, что 
, 
, 
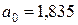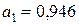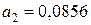. Таким образом, получили уравнение множественной регрессии 
.
Коэффициенты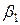 
и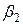 
стандартизованного уравнения регрессии 
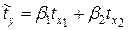находятся по формулам (предварительно вычислим 
, 
, 
):
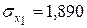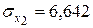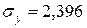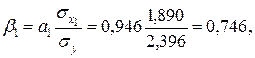
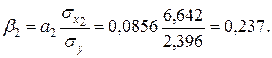
Следовательно, уравнение множественной линейной регрессии в стандартизованном масштабе имеет вид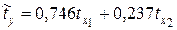 
. Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что ввод в действие новых основных фондов оказывает большее влияние на выработку продукции, чем удельный вес рабочих высокой квалификации.
Ранжировать влияние факторов на переменную можно также при помощи средних коэффициентов эластичности. Они рассчитываются по формуле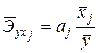 
, 
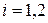. Так как 
, 
, 
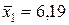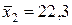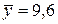, то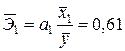 
, 
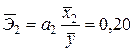. Следовательно, увеличение основных фондов (от своего среднего значения) на 1% увеличивает в среднем выработку продукции на 0,61%. Увеличение удельного веса рабочих высокой квалификации (от своего среднего значения) на 1% увеличивает в среднем выработку продукции 0,20%. Таким образом, и средние коэффициенты эластичности подтверждают большее влияние на результат фактора 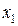по сравнению с фактором .
|
|
|
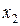2) Рассчитаем сначала парные коэффициенты корреляции:
,
, 
.
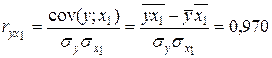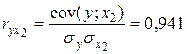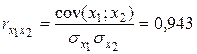Они указывают на весьма сильную связь каждого фактора с результативным признаком , а также высокую межфакторную зависимость (факторы 
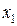и 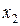явно коллинеарны, т.к. 
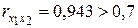). При такой сильной межфакторной зависимости рекомендуется один из факторов исключить из рассмотрения.
Этим фактором должен быть фактор 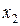, так как: 1) стандартизованный коэффициент для фактора 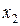меньше, чем для 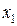; 2) средний коэффициент эластичности для фактора 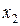меньше, чем для 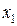; 3) коэффициент корреляции 
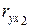меньше коэффициента корреляции 
.
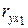Коэффициент множественной корреляции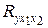 
вычисляется по формуле
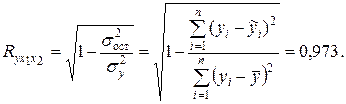
Он характеризует тесноту совместного влияния факторов на результат: совокупная связь факторов с результативным признаком весьма высокая. Значение коэффициент множественной корреляции незначительно отличается от коэффициента парной корреляции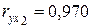 
.
Общий вывод состоит в том, что множественная модель с факторам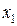и и 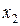содержит малоинформативный фактор 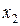. Если исключить фактор 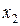, то можно ограничиться уравнением парной регрессии, которое имеет вид 
.
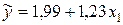3) Для вычисления коэффициента детерминации воспользуемся формулой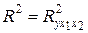 
. Величина 
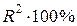показывает, что изменения выработки продукции на одного работника на 94,7% объясняются изменением факторных признаков, включенных в модель.
Отметим, что в случае парной линейной связи коэффициент детерминации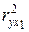 
равен 0,941. Таким образом, изменения выработки продукции на одного
работника на 94,1% объясняются изменением фактора .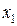
Наблюдаемое значение статистики Фишера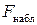 
вычисляется по выборочным данным на основании формулы 
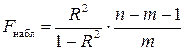, где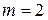 
– число объясняющих переменных в модели, а 
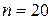– число наблюдений. В нашем случае имеем 
.
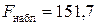По таблицам критических точек 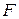-распределения находится критическое значение статистики 
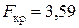при заданном уровне значимости 
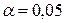. При этом число степеней свободы определяется значениями 
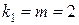и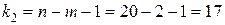 
. Так как 
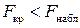, то уравнение множественной регрессии признается статистически надежным.
4) Гипотеза о статистической значимости коэффициентов линейной множественной регрессии проверяется с помощью t- статистики, имеющей распределение Стьюдента с числом степеней свободы, равным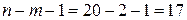 
.
Наблюдаемые значения t- статистики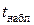 
для коэффициентов регресси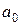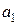и , и 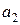равны 3,9, 4,45 и 1,42 соответственно. Табличное значение 
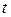-статистики 
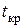равно 2,1. Так как для коэффициентов регресси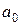и и 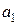выполняется неравенство 
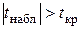, то признается, что коэффициенты 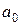и 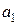линейного уравнения регрессии не случайно отличаются от нуля, а значит, они статистически значимы. Так как для коэффициента 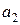выполняется неравенство 
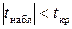, то коэффициент регрессии 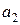статистически не значим. Это дает нам дополнительные основания для того, чтобы исключить фактор 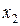из уравнения множественной регрессии и перейти к уравнению парной линейной регрессии с регрессором .
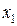Пример 4.5. На основании статистических данных, представленных в таблице 4.8, построена линейная модель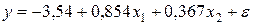 
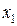, устанавливающая зависимость сменной добычи угля в шахтах на одного рабочего (т) от мощности пласта (м) и уровня механизации (%).
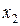По построенной модели осуществить точный прогноз добычи угля на одного рабочего в шахте, где мощность пласта составляет 8 м, а уровень механизации равен 6%. Вычислить доверительный интервал прогноза с доверительной вероятностью 0,95.
Таблица 4.8. Статистические данные задания 4.5
| ||||||||||
| ||||||||||
|
|
Решение:
Обозначим
, 
.
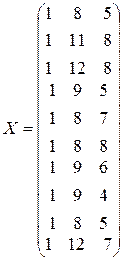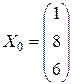Точечный прогноз найдем по уравнению регрессию:
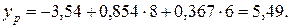
Стандартную ошибку регрессии определим по формуле (4.4)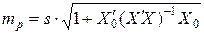 
, где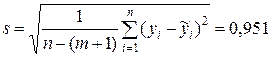 
.
Вычислив обратную матрицу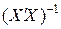 
и выполнив последовательно умножение соответствующих матриц, получим 
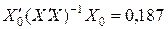. Значит, 
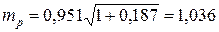. Так как 
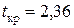, то доверительный интервал прогноза имеет вид 
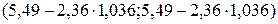, т.е. вид 
.
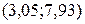Следовательно, с доверительной вероятностью 0,95 значение сменной добычи угля в шахте, где мощность пласта составляет 8 м, а уровень механизации равен 6%, находится в пределах от 3,05 до 7,93 тонны.
