Формулы для многочленов и операции над многочленами

Напомним какое выражение называется многочленом.

Одночленом степени 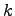(здесь 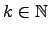) называется следующее выражение

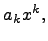
где 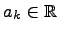-- коэффициент, 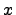- переменная.

Многочленом 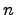- ой степени (здесь 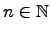) с вещественными коэффициентами 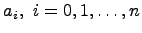называется следующее выражение:

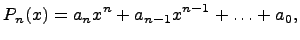
здесь 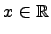- переменная. Можно сказать, что многочлен - это линейная комбинация одночленнов разных степеней.

Операции над многочленами:

Пусть 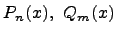два многочлена степен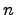и и 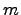соответственно, т.е.

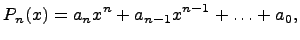
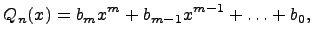
предположим, что .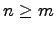

1. Сумма и разность многочленов: .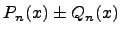

Суммой и разностью многочленов 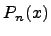и 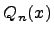называется следующий многочлен:

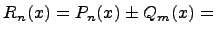
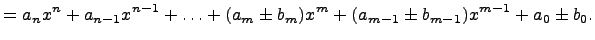
Степень полученного многочлена 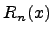не превосходит максимальной степени многочленов 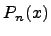и .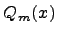

2. Умножение на одночлен: .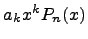

Умножим одночлен 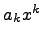на многочлен :

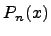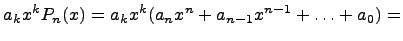
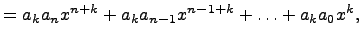
т.е. каждый член многочлена умножается на одночлен. Здесь применяем правило работы со степенями.

3. Умножение многочленов: .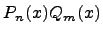

Умножим многочлен 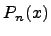на :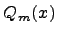

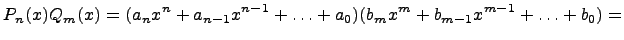
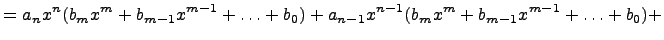
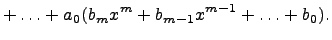
В итоге свели операцию умножения многочленов к умножению одночлена на многочлен. Заметим, что при умножении многочленов степен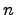и и 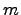получается многочлен степени 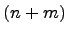. При умножении многочленов необходимо каждый член одного многочлена умножить на каждый член другого многочлена.

4. Деление многочленов: .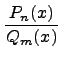

Разделим многочлен 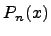на 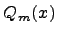, т.е. представим выражение 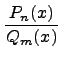в следующем виде:

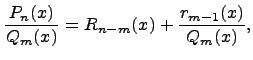
где 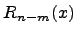-- частное от деления, 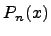-- делимое, 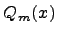-- делитель, 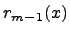-- остаток.

При делении многочлена 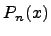на многочлен 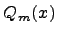, где 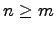, нужно найти многочлены 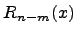и 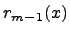такие, чтобы выполнялось равенство

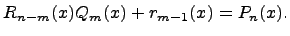
Существует много способов поиска таких многочленов. В основном используются школьные способы, а именно, деление "уголком" ("столбиком") и метод неопределенных коэффициентов (будут рассмотрены ниже).