2015-02-27
935
Теорема 1.8 (формула вычисления векторного произведения). Если векторы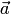 
и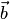 
в правом ортонормированием базисе 
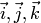имеют координаты 
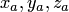и 
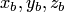соответственно, то векторное произведение этих векторов находится по формуле (1.15), которую принято записывать в виде
| (1.16) |
Есл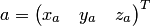и 
и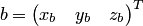 
— координатные столбцы векторов 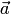и 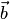в стандартном базисе, то координатный столбец 
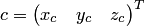векторного произведения 
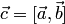находится по формуле
В самом деле, выполняя умножение матрицы на столбец, получаем
Тогда, что совпадает с (1.15).
Пример 1.20. Параллелограмм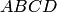 
построен на векторах (рис. 1.46). Найти:
а) векторные произведения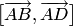 
и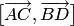 
;
б) площадь параллелограмма ;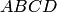
в) направляющие косинусы такого вектора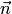 
, перпендикулярного плоскости параллелограмма ,
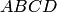для которого тройка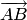 
, 
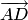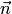, — левая.
Решение. а) Векторное произведение 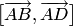находим по формуле (1.16):
Для нахождения векторного произведения можно использовать матричную запись формулы (1.15) (см. теорему 1.8). Векторам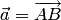 
и 
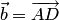соответствуют координатные столбцы 
.
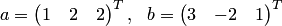По указанной формуле получаем координатный столбец 
вектора :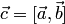
то есть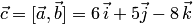 
. Результаты совпадают.
Векторное произведение 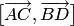находим, используя алгебраические свойства:
Следовательно,.
б) Площадь параллелограмма 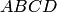находим как модуль векторного произведения :
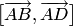в) Вектор, противоположный вектору 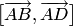, удовлетворяет перечисленным в условии требованиям, поэтому
Разделив этот вектор на его длину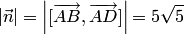 
, получим единичныи вектор:
Согласно его координатами служат направляющие косинусы
51. Мішаний добуток векторів, його властивості та геометричний зміст. Необхідна та достатня умова компланарності векторів. Обчислення мішаного добутку.
