Пусть дан интеграл 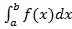 , где функция
, где функция 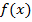 непрерывна на отрезке
непрерывна на отрезке 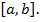 Введем новую переменную
Введем новую переменную 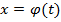 .
.
Теорема 4. Пусть функция 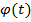 дифференцируема на отрезке
дифференцируема на отрезке 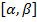 , причем
, причем 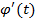 непрерывна на
непрерывна на 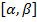 и
и 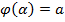 ,
, 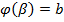 . Тогда справедлива формула
. Тогда справедлива формула
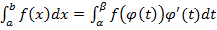 . (13)
. (13)
Формула (13) называется формулой интегрирование подстановкой или замены переменной.
Доказательство. Пусть 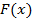 и
и 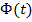 -некоторые первообразные для функций
-некоторые первообразные для функций 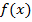 и
и 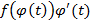 . Тогда из теоремы Лагранжа найдется такое число
. Тогда из теоремы Лагранжа найдется такое число 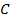 , что
, что 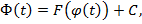 где
где 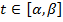 . Поэтому
. Поэтому
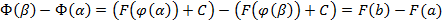 .
.
Но по формуле Ньютона-Лейбница 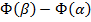 совпадает справой частью (13), а
совпадает справой частью (13), а 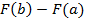 - с левой частью (13).
- с левой частью (13).
Пример. 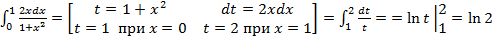 .
.
 2015-02-27
2015-02-27 1168
1168








