 Пусть дано уравнение f(x)=0, где функция f(x) непрерывна на отрезке [a, b]. Отрезок [a, b] содержит изолированный корень, тогда f(a)*f(b)<0. Для нахождения корня уравнения, принадлежащего отрезку [a, b], делим отрезок пополам.
Пусть дано уравнение f(x)=0, где функция f(x) непрерывна на отрезке [a, b]. Отрезок [a, b] содержит изолированный корень, тогда f(a)*f(b)<0. Для нахождения корня уравнения, принадлежащего отрезку [a, b], делим отрезок пополам.
c= 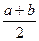 (1.3)
(1.3)
Если f(c)=0, то ξ=(a+ b)/2 является корнем уравнения.
Если f(c)≠0, то выбираем ту из половинок [a, c] или [c, b], на концах которой функция имеет противоположные знаки, т. е. f(a)*f(c)<0 (f(c)*f(b)<0).
Выбранную половину вновь делим пополам, повторяя те же рассуждения, и т. д. Процесс дробления отрезка прекращаем при условии │an-bn│≤ε, где ε- заданная погрешность, тогда приближенное значение корня определяется по формуле:
x0= 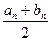 (1.4)
(1.4)
В результате получаем последовательность вложенных друг в друга отрезков [a, b], [a1, b1], [a2, b2],…,[an, bn]… таких, что
f(an)*f(bn)≤0 (n=1, 2,…) (1.5)
где bn-an= 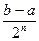 . (1.6)
. (1.6)
Так как левые концы a, a1, a2,…an образуют монотонно возрастающую последовательность, а правые b, b1, b2,…bn – монотонно убывающую, то,в силу равенства (1.6), получим предел
ξ= 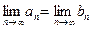 (1.7)
(1.7)
Тогда неравенство (1.5) будет иметь вид f(ξ)2≤0, т. е. f(ξ)=0, следовательно, ξ является корнем уравнения.
|
|
|
Геометрическая интерпретация метода показана на рисунке 5.
y
 |

 f(b)
f(b)


 a с ξ b x
a с ξ b x
f(a) f(c)
Рис. 5
 2015-02-27
2015-02-27 663
663








