Лекция 5. Аналитические методы моделирования объектов с сосредоточенными параметрами

Содержание лекции:

- аналитические методы моделирования объектов с сосредоточенными параметрами.

Цель лекции:

- изучить на примерах основные методы аналитического моделирования объектов с сосредоточенными параметрами.

При составлении дифференциальных уравнений объектов с сосредоточенными параметрами обычно исходят из уравнений материального и теплового баланса.

Согласно первому из них изменение массы вещества в замкнутом объеме в единицу времени равно алгебраической сумме входных и выходных потоков

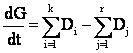(5.1)

здесь: D_i (i=1,k) – массовый расход входного i-го потока, D_j (j=1,r) - массовый расход выходного j-го потока, G – масса вещества в рассматриваемом объеме, t - время.

Аналогично, изменение энтальпии какого-либо тела в единицу времени равно алгебраической сумме тепловых потоков, подводящих (или отводящих) тепло к рассматриваемому телу

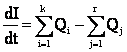(5.2)

где Q_i (i=1,k) – i-ый входной поток тепла, Q_j (j=1,r) - j-ый выходной поток тепла, I – энтальпия тела.

Дать законченную теорию моделирования всех разновидностей процессов в их различных проявлениях не представляется возможным. Для иллюстрации применения основных естественнонаучных законов сохранения массы, движения, энергии в наиболее характерных процессах рассмотрим несколько примеров.

Пример 5.1. Моделирование объекта регулирования уровня жидкости в резервуаре.

Объектом исследования является резервуар с независимым G_n(t) притоком жидкости и зависимым стоком G_c(t). Последний определяется величиной уровня над сливным отверстием H и площадью проходного сечения сливного отверстия f_c.

При составлении уравнений математической модели объекта используются:

- уравнение материального баланса системы:

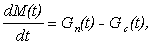(5.3)

- уравнение, отражающее закон сохранения движения; G_с не является независимой переменной, это функция М. В соответствии с законом гидродинамики поток из выходного отверстия определяется законом

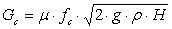(5.4)

здесь μ – кэффициент расхода, f_c - площадь поперечного сечения выходного отверстия, g - ускорение свободного падения, H - уровень жидкости в резервуаре.

а) Требуется изучить поведение объекта в условиях равновесия, под которым будем понимать неизменность координат состояния (здесь Н и G_c) во времени. Нетрудно видеть, что при равновесии в резервуаре не будет происходить изменения количества вещества, то есть 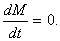Следовательно, уравнение материального баланса будет выражено очевидным соотношением

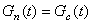
С другой стороны, понятие равновесия с математической точки зрения выражается равенством нулю всех производных координат состояния

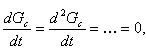отсюда имеем .

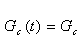А это, в свою очередь, означает, что

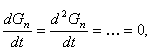или .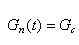

В итоге можно записать

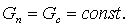(5.5)

Подставляя (5.4) в (5.5) получим возможность вычислять положение уровня жидкости в баке

.

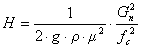Таким образом, математическая модель системы, находящейся в равновесии, может быть представлена в виде

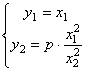или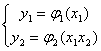

где - x₁ = G_n, x₂ = f_c; y₁ = G_c, y₂ = H - переменные, P = 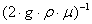- параметр модели.

Эта модель – статическая, название связано со статичным состоянием объекта, находящегося в равновесии.

б) Требуется изучить поведение бака с жидкостью в общем случае, снимая условия равновесия.

Количество жидкости в резервуаре, находящейся над плоскостью сливного отверстия, определяется из соотношения:

,

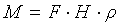где F – площадь поперечного сечения резервуара, ρ – плотность.

Считая F и ρ постоянными, то есть принимая F=F₀, ρ= ρ₀ и подставляя вместо 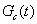его выражение (5.4), получим дифференциальное уравнение:

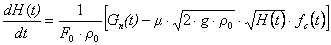. (5.6)

Это уравнение в обобщенной форме может быть записано следующим образом:

.

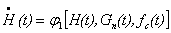Соотношение (5.4) можно привести к обобщенной форме

.

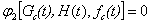В итоге система двух уравнений с двумя неизвестными:

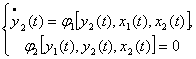(5.7)

является динамической моделью резервуара с жидкостью. При этом динамика связывается с изменением состояния системы.

В этом примере статическая модель является частным случаем динамической модели. Это обстоятельство не является обязательным. Чаще всего, два этих типа моделей дополняют друг друга.

в) Требуется получить линеаризованную динамическую модель резервуара с жидкостью, считая, что исходное состояние равновесия системы соответствует времени t₀.

Для оценки значений координат состояния в начальном состоянии равновесия можно воспользоваться статической моделью. Тогда

.

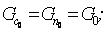
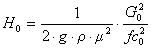Основную нелинейность в систему уравнений вносит соотношение (5.4). Разложим его в ряд Тейлора, ограничиваясь только линейными членами:

(5.8)

Определим коэффициенты ряда:

.

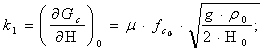
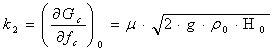Принимая во внимание исходное состояние равновесия, будем в модели изучать только отклонения переменных от своих начальных значений, то есть:

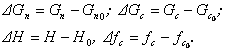(5.9)

Тогда:

.

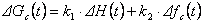Это уравнение является первым уравнением линеаризованной модели. Подставим результат линеаризации (5.8) в (5.6) и, имея ввиду, что

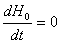и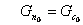

получим:

.

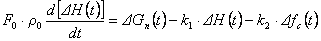Используя обозначения:

y_{1 =} ΔG_с, y₂ = ΔΗ, x₁ = ΔG_n и x₂ = Δf_c,

линеаризованную динамическую модель бака с жидкостью можно представить следующей системой уравнений:

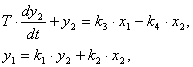
в которой

.

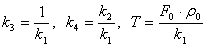Коэффициенты уравнений k_i и T, являющиеся параметрами линеаризованной модели, зависят от состояния равновесия, предшествующего переходному процессу. Поэтому модель требует перенастройки ее параметров в случае изменения исходных состояний ( 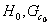) моделируемого объекта.

В случае необходимости моделирования объекта при существенном изменении крутизны характеристик переходят к их кусочно-линейной аппроксимации. При этом нелинейный объект описывается совокупностью линейных зависимостей и логических соотношений, определяющих зону действия каждого линейного выражения.