Содержание лекции. Метод точечных преобразований позволяет определить существование автоколебаний в нелинейной системе

Метод точечных преобразований позволяет определить существование автоколебаний в нелинейной системе, устойчивость или неустойчивость предельного цикла без построения фазовых траекторий. Известно, что нелинейные системы в большинстве случаев описываются сложными дифференциальными уравнениями. Поэтому целесообразно провести не всё построение фазовой траектории, а рассмотреть изменение фазовой траектории того участка, описание которого можно сделать по приближенному линейному дифференциальному уравнению без особых затруднений. Затем по этому отдельному участку можно судить о возможности или невозможности возникновения автоколебаний. В принципе, этот метод пригоден для системы любого порядка, но если порядок дифференциального уравнения выше третьего, то возникают трудности в расчёте.

Рассмотрим применение этого метода для системы второго порядка с трёхпозиционным реле с гистерезисом (рис. 2.15). Фазовая траектория это системы показана на рис. 2.16.

Чтобы исследовать динамику системы по этому методу, необходимо выяснить, как в зависимости от начальных условий перемещается точка М0 по оси абсцисс. Для этого вся фазовая траектория (см. рис. 2.16) разделяется на отдельные участки:

I участок. От значения x > a2, когда реле включено (+b) до отключения реле при xвх = a1 (см. рис. 2.16)

Рис.2.15. Трехпозиционное реле с гистерезисом

Рис.2.16. Фазовая траектория системы с трехпозиционным реле

II и VI участок. Реле отключено; движение системы за счёт инерционности системы.

III участок. Реле включается с противоположным знаком своей выходной величины (-b) при x < - a2..

I участок. Реле снова включилось (+b) при xвх > a2.

Из всех участков рассмотрим изменение фазовой траектории на оси +x. Допустим, что начальное положение изображающей точки системы М 0, где х(0) = х 0. Изображающая точка будет двигаться по соответствующим траекториям и снова приходит на ось + х в точку М 0*,где х * < х 0. Если при любых значениях х0 оказывается, что х * всегда меньше х 0, то система имеет затухающий и поэтому устойчивый переходный процесс. Но если х * > х 0, то это свидетельствует о расходящемся и поэтому неустойчивом процессе. Возможен и третий случай, когда при заданном х0 получаем равенство х * = х0. Система снова вернулась в исходное состояние. Это значит, что система имеет предельный цикл (автоколебания). Сразу возникает вопрос: эти автоколебания устойчивые или неустойчивые? По методу точечных преобразований это решается достаточно просто.

Пусть свободное движение системы при включённом реле на участке I

описывается уравнением

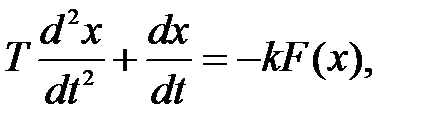
где F(x) – характеристика реле.

Уравнение фазовой траектории x=T kF(x) ln(y – kF(x)) – Ty + C₀,

где С₀ – начальные условия.

Пусть начальные условия C₀ соответствуют значениям x₀ и y₀. Уравнение фазовой траектории на участке 1 с учетом этих начальных условий при F(x)=b

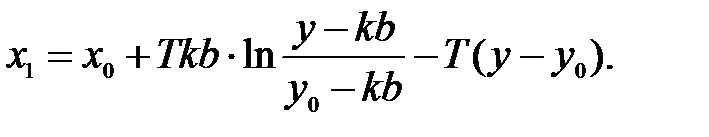
Рассмотрим на участке 1 изменение положения точки M₀ (при x(0)=x₀, y(0)=0) до M₀^’ (при x₁, y=0). Это характеризует изменение координаты по оси x на величину Δx (при F(x)=b и y=0).

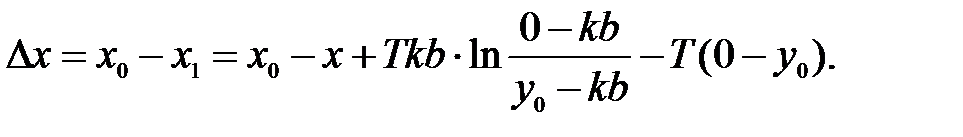
Изменение положения точки М0. не зависит от y. Величина y для обоих значений М0 и М0 равна 0. Это изменение Δx зависит от начального значения х0. В результате получаем зависимость x1 = f(x0).

Для анализа системы строим график, где ось абсцисс – состояние системы выраженное через начальное значение точки х0. Ось ординат – вычисленное значение точки х1 (рис. 2.17).

На этом графике проводим биссектрису координатного угла, т.е. прямую под углом 45⁰. Эта биссектриса характеризует те точки фазовой траектории где х0i = х1 или те значения х0i, когда фазовая траектория возвращается в первоначальное состояние (предельный цикл). Возможны следующие случаи взаиморасположения кривой х1 = f(х0) и прямой х1= х0.

1. Кривая х1 = f(х0) расположена справа от прямой х0 = х1 и её не пересекает (рис. 2.17). При любом начальном значении х0 процесс сходящийся к конечному значению х0*. Система устойчива “в общем”.

Рис.2.17. Характеристика x₁=f(x₀) справа от x₁=x₀

2. Кривая х₁ = f(х0) расположена справа от х0 = х1 и её касается в точке N1 (рис. 2.18). При х0 > C1 процесс сходится к полуустойчивому предельному циклу в точке N1 и легко может сойти с него. При х0 < C1 процесс сходится к значению х0*. Система устойчива “в общем”, но возможен режим автоколебаний при х0 = С1.

3. Кривая х1 = f(х0) и прямая х0 = х1 имеют две точки пересечения N1 и N2. (рис. 2.19). Возможны три варианта поведения системы:

– при х01 < С1 система движется к значению х0*. Система устойчива

“в малом”;

– при С1 < х02 < С2 система движется к N2. Значение х1 = f(х0) увеличивается. Система неустойчива “в малом”, величина х02 возрастает до С2, где х0** = С2 – устойчивый предельный цикл. Система устойчива “в большом”;

– при х03 > С2 система возвращается к значению N2, величина х03 уменьшается до х**0 = С2. Система тоже устойчива “в большом”. Система имеет два предельных цикла. При х0 = С1 неустойчивый предельный цикл (точка N1). При х0 = С2 устойчивый предельный цикл (точка N2).

Рис.2.18. Характеристика x₁=f(x₀) касается x₁=x₀

Рис.2.19. Характеристика x₁ = f(x₀) пересекает x₁ = x₀ в двух точках

4. Кривая х1 = f(х0) имеет одну точку пересечения N1 (рис. 2.20). Устойчивость системы зависит от значения х0 относительно C1:

– при х01 < C1 система движется к *0 x. Система устойчива “в малом”

– при х02 > C1 значение х0 возрастает. Система неустойчива “в большом”. Система имеет один неустойчивый предельный цикл в точке N1.

Рис.2.20.. Характеристика x₁ = f(x₀) пересекает x₁ = x₀ в одной точке

5. Кривая х1 = f(х0) имеет одну точку пересечения N 2 (рисунок 2.21). При любом значении х0 система стремится к точке N2. Если х01 < C1, то значение х0 увеличивается до х0 = C2. Система неустойчива “в малом”. Если х02 > C1, то значение х0 уменьшается до х0 = C1. Система устойчива “в большом”. Она имеет один устойчивый предельный цикл в точке N2 при х0= C1.

Рис.2.21.. Характеристика x₁ = f(x₀) пересекает x₁ = x₀ в одной точке

6. Кривая х1 = f(х0) расположена слева от прямой х1 = х0 и нигде не пересекается (рисунок 2.22). Если нет точки пересечения, то нет предельного цикла. При любом значении х0 значение x1 = f(х0) увеличивается. Система неустойчива “в малом” и “в большом”, она неустойчива “в общем”.

Такой расчёт можно сделать по изменению скорости движения системы y1 = f (y0) относительно y1 = y0, Это зависит от того, на каком участке движение системы проще получить и анализировать уравнение фазовой траектории.

Рис.2.22. Характеристика x₁ = f(x₀) слева от x₁ = x₀

Контрольные вопросы для самоподготовки

1. Что можно определить методом точечных преобразований?

2. В чем преимущество анализа системы методрм точечных преобразований?

3. При каком взаимном расположении кривой x₁ = f(x₀) и прямой x₁ = x₀ система устойчива «в общем»?

4. При каком взаимном расположении кривой x₁ = f(x₀) и прямой x₁ = x₀ система неустойчива?

5. При каком взаимном расположении кривой x₁ = f(x₀) и прямой x₁ = x₀ система устойчива «в малом» и неустойчива «в большом»?

6. При каком взаимном расположении кривой x₁ = f(x₀) и прямой x₁ = x₀ система неустойчива «в малом» и устойчива «в большом»

7. Что характеризует прямая x₁ = f(x₀)?

8. Как выбирается участок фазовой траектории для анализа систем методом точечных преобразований?