При исследовании динамических свойств систем автоматического управления классическими методами после составления дифференциальных уравнений для отдельных элементов системы обычно переходят к передаточным функциям этих элементов. Далее составляют общую структурную схему для всей системы, в которой отдельные элементы представляются блоками с соответствующими передаточными функциями. Затем определяется передаточная функция замкнутой системы, характеризующая связь между изображениями по Лапласу входной и выходной величин.
Поведение системы во времени можно характеризовать не только выходной функцией системы, но и промежуточными переменными в цепи системы, число которых равно порядку системы n. Таким образом, получается n -мерный вектор состояния, множество возможных положений которого образует векторное пространство, называемое пространством состояний системы. Процедура нахождения значений некоторой функции y(t) для будущих моментов времени называется прогнозированием (предсказанием). Возможность предсказания является естественным требованием качественного управления. Основанием для построения алгоритмов прогнозирования поведения системы в любой момент времени 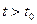 (и управления неавтономной системой) достаточно информации о переменных состояния в момент
(и управления неавтономной системой) достаточно информации о переменных состояния в момент 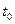 и не требуется знание предыстории процессов, т.е. информации о функциях
и не требуется знание предыстории процессов, т.е. информации о функциях 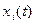 при
при 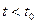 .
.
|
|
|
Метод занимает центральное место в современной теории управления, так как предоставляет широкие возможности формализации процедур анализа, синтеза и автоматизации проектирования.
Состояние системы – это совокупность таких значений переменных, знание которых, наряду с входными функциями и уравнениями, описывающими динамику системы, позволяет определить её будущее состояние и выходную переменную.
Переменными состояния динамической системы с выходом y(t) называется множество переменных xi (t) таких, что значение выходной переменной y(t) в произвольный момент времени ti однозначно определяется, если заданы xi(t0) и u[t0,t1].
Выбор переменных состояния динамической системы неоднозначен. Обычно вводят
фазовые переменные, т. е. используют в математическом описании объекта
n – переменных 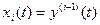 ,
, 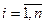 . В качестве переменных состояния могут быть
. В качестве переменных состояния могут быть
взяты физические переменные системы, такие как перемещение, скорость, ток,
напряжение, а также n других независимых функций времени, полученных как
линейные комбинации фазовых и/или физических переменных. Выбор переменных
состояния определяет структуру и параметры модели вход – состояние – выход.
Для неавтономных систем с помощью переменных состояния устанавливается
|
|
|
однозначное соответствие между входными и выходными воздействиями.
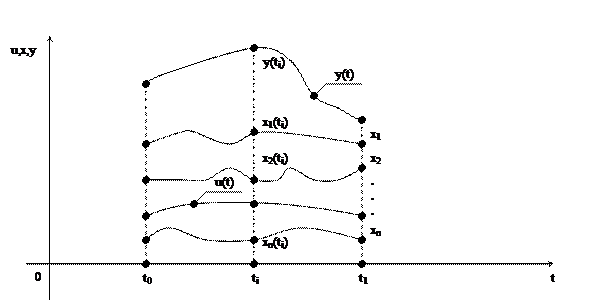
Вектор 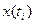 является элементом n – мерного линейного векторного пространства
является элементом n – мерного линейного векторного пространства 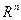 ,
, 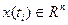 ,
, 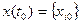 - вектор начальных условий (начального состояния).
- вектор начальных условий (начального состояния).
 |
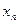
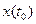

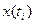


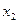
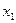
Пространством состояний называется метрическое пространство 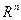 , каждый элемент которого полностью определяет состояние системы (процесса) в текущий или заданный момент времени.
, каждый элемент которого полностью определяет состояние системы (процесса) в текущий или заданный момент времени.
Понятие «состояние системы» является одним из базовых (фундаментальных) понятий теории динамических систем, поэтому его следует определять не через другие понятия, а аксиоматически, т. е. перечислением совокупности присущих ему свойств:
1. Аксиома 1. Выход y(t) для всех 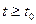 определяется однозначно, если заданы x(t0) и u[t0,t1);
определяется однозначно, если заданы x(t0) и u[t0,t1);
2. Аксиома 2. Если траекторию системы разбить на ряд участков, то можно рассматривать движение на каждом из них как новую траекторию при соответствующем начальном состоянии;
и др. в кн. Заде Л., Дезоер Ч. Теория линейных систем. Метод пространства состояний. – М.: Наука, 1970.
Состояние системы описывается системой дифференциальных уравнений первого порядка относительно каждой из переменных состояния в форме Коши:
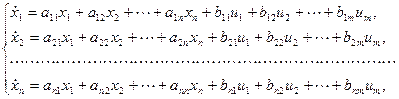
в матричной форме (нормальная форма уравнения состояния):
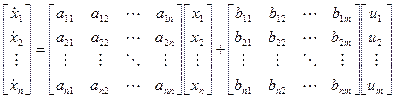 - матричная форма дифференциального уравнения (абстрактная, формально – алгебраическая структура современной теории управления).
- матричная форма дифференциального уравнения (абстрактная, формально – алгебраическая структура современной теории управления).
или (модель вход – состояние – выход)
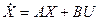 - уравнение состояния (модель вход – состояние),
- уравнение состояния (модель вход – состояние),
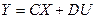 - уравнение выхода (модель состояние – выход).
- уравнение выхода (модель состояние – выход).
А – матрица коэффициентов (квадратная, параметрическая матрица Сильвестра должна быть обратима) системы,
В – матрица входа,
С – матрица выхода,
D – матрица обхода системы,
Х – вектор состояния,
U – вектор входных воздействий (управляющих и возмущающих),
Y – вектор выходных функций.
Модель системы в форме структурной схемы имеет вид
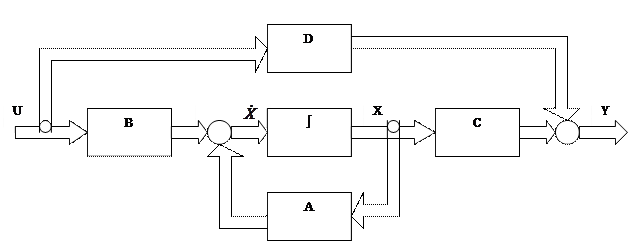
Общий принцип построения схем моделирования заключается в формировании структурной схемы, состоящей только из интеграторов, сумматоров и коэффициентов усиления.
Если схема моделирования строится на основе дифференциальных уравнений системы, то решение является однозначным. Если исходные данные представлены в виде передаточной функции, то схема моделирования может иметь различную конфигурацию, т. е. решение уже не будет однозначным.
Решение матричного уравнения стационарной автономной системы может быть представлено в виде:
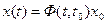 ,
,
где 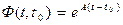 - фундаментальная (переходная) матрица системы.
- фундаментальная (переходная) матрица системы.
Подставляя это уравнение в уравнение выхода системы, получим выражение для расчёта выходной функции
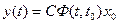 .
.
Если для некоторых начальных условий и любых 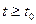 имеет место тождество
имеет место тождество
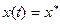 ,
,
где 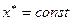 , то значение
, то значение 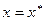 называется равновесным состоянием или положением равновесия автономной системы.
называется равновесным состоянием или положением равновесия автономной системы.
Очевидно, что в равновесном состоянии выполняется
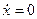 ,
,
и, следовательно,
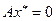 .
.
При условии, что 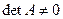 , получаем, что единственным положением равновесия системы является начало координат пространства состояний
, получаем, что единственным положением равновесия системы является начало координат пространства состояний 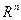 , т.е.
, т.е.
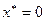 .
.
При 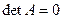 существуют нетривиальные множества равновесных состояний (прямые, плоскости), т.е. подпространства, удовлетворяющие уравнению
существуют нетривиальные множества равновесных состояний (прямые, плоскости), т.е. подпространства, удовлетворяющие уравнению 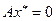 .
.
После подстановки 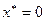 в уравнение выхода
в уравнение выхода 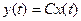 находим равновесное значение выходной переменной
находим равновесное значение выходной переменной 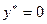 .
.
Графически 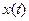 представимы в виде:
представимы в виде:
● временных диаграмм;
● фазовых траекторий (интегральных кривых).
Фазовой траекторией, или интегральной кривой в 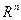 , называется линия, описываемая вектором состояния
, называется линия, описываемая вектором состояния 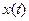 в пространстве состояний
в пространстве состояний 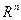 при изменении переменной
при изменении переменной 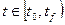 ,
, 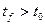 , т.е. годограф вектор – функции
, т.е. годограф вектор – функции 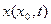 по параметру
по параметру 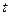 .
.
Фазовый портрет – это множество фазовых траекторий, соответствующих различным значениям начальных условий 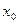 .
.
Введенные выше понятия обобщаются на класс многоканальных (многосвязных) систем, которые характеризуются несколькими выходными переменными 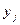 ,
, 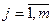 .
.
|
|
|
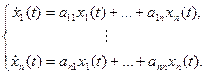
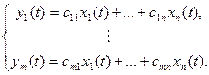
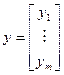 - вектор пространства выходных
- вектор пространства выходных
функций в 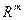 .
.
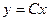 , где
, где 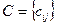 - матрица размера
- матрица размера 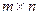 .
.
Переходные процессы:
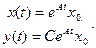
Определим следующие алгебраические объекты:
● характеристический полином матрицы состояния A:
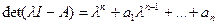 ;
;
● собственные значения (собственные числа) матрицы A как n чисел 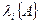 ,
,
являющихся корнями характеристического полинома;
● собственные векторы матрицы 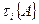 .
.
Полагая 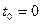 , решение уравнения системы можно представить в виде
, решение уравнения системы можно представить в виде
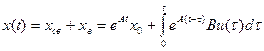 ,
,
где 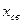 - свободная составляющая (переходный процесс автономной системы), соответствующая решению однородного дифференциального уравнения и зависящая от начальных условий
- свободная составляющая (переходный процесс автономной системы), соответствующая решению однородного дифференциального уравнения и зависящая от начальных условий 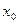 ,
,
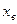 - вынужденная составляющая, соответствующая переходному процессу системы при нулевых начальных условиях
- вынужденная составляющая, соответствующая переходному процессу системы при нулевых начальных условиях 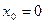 (реакция системы на входное воздействие).
(реакция системы на входное воздействие).
Уравнение выхода
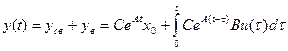 .
.
Матрица 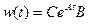 является весовой (импульсной переходной) матрицей.
является весовой (импульсной переходной) матрицей.
 2015-03-22
2015-03-22 12790
12790








