Один из методов решения дифференциального уравнения заключается в следующем. Считают, что решение имеет вид бесконечного ряда с неизвестными коэффициентами. Этот ряд подставляют в дифференциальное уравнение и таким образом определяют неизвестные коэффициенты. Воспользуемся данным методом для нахождения матрицы перехода. В предположении, что все входные переменные системы равны нулю, уравнение состояния принимает вид
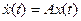 , (1)
, (1)
а его решение
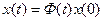 . (2)
. (2)
Поскольку искомым является вектор 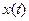 , представим его в виде ряда:
, представим его в виде ряда:
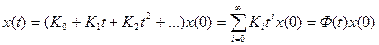 , (3)
, (3)
где все матрицы 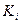 размерности
размерности 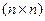 считаются неизвестными, а
считаются неизвестными, а 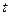 - скалярная переменная (время).
- скалярная переменная (время).
Дифференцируя это выражение, получим:
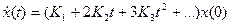 . (4)
. (4)
Подставим (3) и (4) в (1):
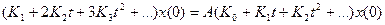 . (5)
. (5)
Далее выполним следующие операции. Сначала вычислим (5) при 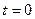 . Затем продифференцируем (5) и найдём результат при
. Затем продифференцируем (5) и найдём результат при 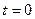 . Ещё раз продифференцируем выражение и подставим
. Ещё раз продифференцируем выражение и подставим 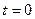 . Повторяя эти действия, каждый раз будем получать уравнение относительно неизвестных матриц
. Повторяя эти действия, каждый раз будем получать уравнение относительно неизвестных матриц 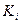 .
.
В итоге образуется система уравнений:
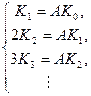 (6)
(6)
Вычисление (3) при 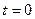 даёт результат
даёт результат 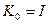 . Тогда другие матрицы определяются из
. Тогда другие матрицы определяются из
|
|
|
уравнений (6):
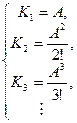 (7)
(7)
Следовательно, матрица перехода, представленная в (3) в виде бесконечного ряда, может быть записана как
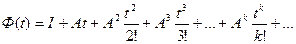 , (8)
, (8)
который сходится для всех конечных 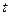 и любой
и любой 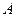 .
.
Сравнивая это выражение с разложением в ряд Тейлора скалярной экспоненты
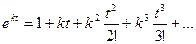 , (9)
, (9)
приходим к выводу, что матрицу перехода можно представить как экспоненциальную функцию матрицы 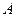 :
:
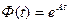 .
.
 2015-03-22
2015-03-22 1259
1259








