К простейшим типам интегрируемых дифференциальных уравнений второго порядка относятся уравнения, для которых функция, стоящая в правой части формулы (12.32), зависит или только от х, или только от у, или только от у',
т.е. уравнения вида:
y'' = f(x); (12.37)
y'' = f(y); (12.38)
y''= f (y'). (12.39)
Общее решение уравнения (12.37) находится двукратным интегрированием.
Уравнение (12.38) интегрируется постановкой
y' = p, (12.40)
которая дает возможность свести его к уравнению с разделяющимися переменными y и p:
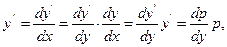
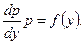
Из последнего уравнения определяется p, а из уравнения y' = p - общий интеграл Ф(x,y,C1,C2) = 0.
Уравнение (12.39) подстановкой (12.40) сводится к уравнению с разделяющимися переменными х и p:
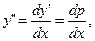
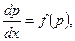
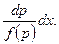
В некоторых случаях дифференциальные уравнения второго порядка сводятся к уравнениям первого порядка.
Уравнение y'' = f(x,y') (12.41)
подстановкой (12.40) приводится к уравнению 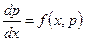
с неизвестной функцией p.
Уравнение y'' = f(y,y') (12.42)
той же подстановкой сводится к уравнению 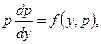
где роль неизвестной переменной играет у.
1. Проинтегрировать уравнение у'' = cos x.
Так как 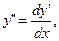 то
то  , dy' = cos xdx,
, dy' = cos xdx,
откуда 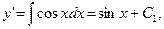
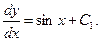
Интегрируя еще раз, получаем:
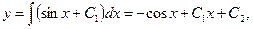
y = - cos x + C1x + C2.
2. Найти общее решение уравнения y'' = 2y'.
Правая часть данного уравнения зависит только от у'. Это уравнение вида (12.39).
Полагая у' = p, находим:
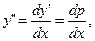
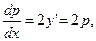
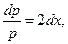
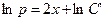 ,
, 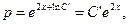
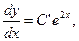
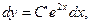
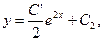
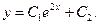
3. Проинтегрировать уравнение
(1+x2)y'' - 2xy' = 0.
Это уравнение вида (12.41), так как в него явно не входит искомая функция y.
Положим y' = p, тогда 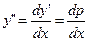
и уравнение принимает вид 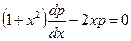 или (1+x2)dp-2xp dx=0.
или (1+x2)dp-2xp dx=0.
Разделяя переменные, получим
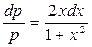
Интегрируя, находим
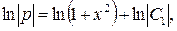 откуда p = C1(1+x2).
откуда p = C1(1+x2).
Так как 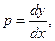 то
то 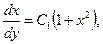 и, следовательно, общее решение определяется формулой
и, следовательно, общее решение определяется формулой 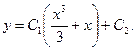
Замечание. Разделяя переменные, мы предполагали, что p ≠ 0,
1+x2 ≠ 0, поэтому могли потерять решения p = 0, 1+x2=0.
Из первого равенства вытекает, что y' = 0 и y = C. Функция y = C является решением исходного уравнения, в чем можно убедиться непосредственно.
Эти решения получаются из общего решения при C1 = 0. Второе равенство невозможно при действительных x, оно не определяет функцию, являющуюся решением данного уравнения.
4. Проинтегрировать уравнение yy''- y' 2=0.
Это уравнение вида (12), так как оно не содержит явно аргумента x.
Положим y' = p, тогда 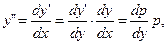
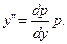
Подставляя выражения для y' и y'' в исходное уравнение, получим
уравнение первого порядка с разделяющимися переменными y и p:
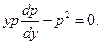
Разделяя переменные, получим
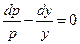 (py≠0).
(py≠0).
Интегрируя, находим
ln|p| = ln|y| + ln|C1|, откуда p = C1y.
Так как p = y', то 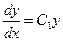 . Интегрируя это уравнение, получаем
. Интегрируя это уравнение, получаем
ln|y| = C1x + ln|C2| или y = C2eC1x.
Замечание. Решения y = 0, y = C (y' = 0) получаются из общего решения соответственно при C2 = 0 и C1 = 0.
Проинтегрировать дифференциальные уравнения второго порядка:
12.51. 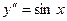
12.54. 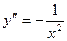
12.57. 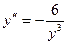
12.52. 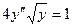
12.55. 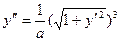
12.58. 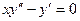
1 12.53. 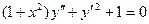
12.56. 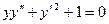
 2015-03-22
2015-03-22 1682
1682








