1. Признак сравнения. Если при x ≥ a выполнены неравенства
0 ≤ j (x) ≤ f (x)
то:
а) из сходимости 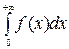 следует сходимость
следует сходимость 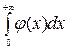 ;
;
б) из расходимости 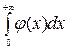 следует расходимость
следует расходимость 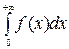 .
.
2. Предельный признак сравнения. Если f(x) и φ(x) непрерывны и знакопостоянны на [ a, ∞ ] и
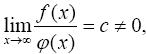
то оба интеграла 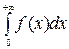 и
и 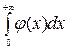 сходятся либо расходятся одновременно.
сходятся либо расходятся одновременно.
3. Абсолютная сходимость. Если несобственный интеграл 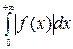
сходится, то сходится и интеграл 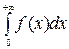 и последний в этом случае называется абсолютно сходящимся.
и последний в этом случае называется абсолютно сходящимся.
Аналогичные признаки имеют место для несобственных интегралов от неограниченных функций.
П р и м е р. Исследовать на сходимость интеграл 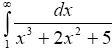
Решение. 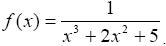 Рассмотрим функцию
Рассмотрим функцию 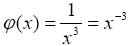
Интеграл 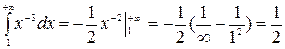 сходится.
сходится.
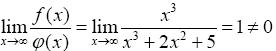
В силу предельного признака сравнения 2 исходный интеграл сходится.
2.8. Геометрические приложения определенного интеграла
1. Вычисление площади плоской фигуры
1.1. Пусть функция f (x) непрерывна и неотрицательна на отрезке [ a, b ]. Тогда площадь фигуры, ограниченной осью ОХ, отрезками прямых x = a, x = b и графиком функции y = f (x), может быть вычислена по формуле 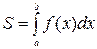 .
.
|
|
|
1.2. Если f 2(x) > f 1(x)на отрезке [ a, b ], f 1(x), f 2(x) − непрерывные функции, то площадь фигуры, ограниченной прямыми х = а, x = b, графиками функций y = f 1(x), y = f 2(x) вычисляется по формуле 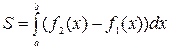 (рис. 10).
(рис. 10).
1.3. Если функция f (x) на отрезке [ a, b ] принимает значения разных знаков, то площадь фигуры, заключенная между кривой y = f (x) и осью OX, равна 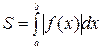 (рис. 11).
(рис. 11).
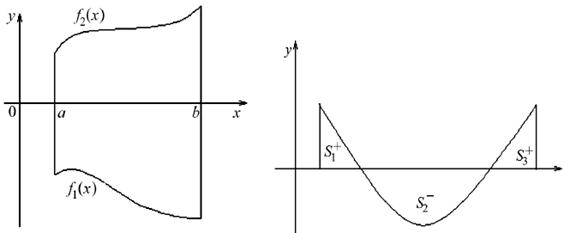
Рис. 10 Рис. 11
П р и м е р. Вычислить площадь фигуры, ограниченной графиками функций y (x) = x и y (x) = 2 − x 2.
Решение. Вычислим координаты точек пересечения графиков этих функций. Для этого решим систему
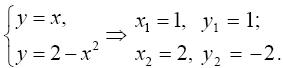
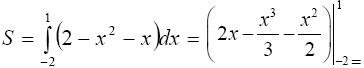
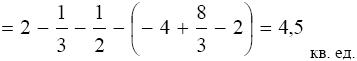
 2015-03-22
2015-03-22 992
992








