3.2.1. Предложение. Если вектор x пространства имеет представление в виде линейной комбинации x=a 1 a 1+ a 2 a 2+…+ akak линейно независимой системы векторов a 1, a 2, …, ak, то это представление единственно.
Из 3.2.1 вытекает
3.2.2. Следствие. Любой вектор x пространства имеет единственное представление в виде
x = x 1 e 1+ x 2 e 2+…+ xnen (3.1)
линейной комбинации базисных векторов e 1, e 2, …, en пространства.
3.2.3. Определение. Коэффициенты x 1, х 2, …, хn линейной комбинации (3.1) вектора x называется координатами вектораxв базисе (e). При этом обозначают x =(x 1, х 2, …, хn). Если мы хотим подчеркнуть, что вектор x задан своими координатами x 1, х 2, …, хn именно в базисе (e), то будем писать x =(x 1, х 2, …, хn) e.
3.2.4. Теорема. Пусть даны векторы x =(x 1, х 2, …, хn) e и y =(y 1, y 2, …, yn) e линейного пространства V. Тогда x + y =(x 1+ y 1, x 2+ y 2, …, xn + yn) e и для любого числа a ax =(ax 1, ax 2, …, axn) e. Другими словами, при сложении векторов их соответствующие координаты складываются, а при умножении вектора на число их координаты умножаются на это число.
Примеры. I. Пусть V - линейное пространство матриц размерности 2´2. Тогда векторы e 1= 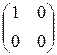 , e 2=
, e 2= 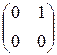 , e 3=
, e 3= 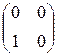 , e 4=
, e 4= 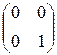 образуют базис этого пространства. Действительно, во-первых, они линейно независимы: из a 1 e 1+ a 2 e 2+ a 3 e 3+ a 4 a 4=0 V следует α 1= α 2= α 3= α 4=0, так как имеет место следующая цепочка равносильностей:
образуют базис этого пространства. Действительно, во-первых, они линейно независимы: из a 1 e 1+ a 2 e 2+ a 3 e 3+ a 4 a 4=0 V следует α 1= α 2= α 3= α 4=0, так как имеет место следующая цепочка равносильностей:
|
|
|
a 1 e 1+ a 2 e 2+ a 3 e 3+ a 4 a 4=0 V Û a 1 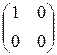 + a 2
+ a 2 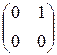 + a 3
+ a 3 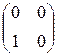 + a 4
+ a 4 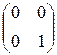 =
= 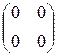 Û
Û
Û 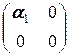 +
+ 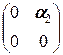 +
+ 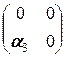 +
+ 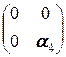 =
= 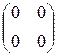 Û
Û 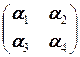 =
= 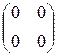 Û
Û 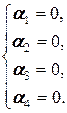
Во-вторых, любой вектор (то есть матрица) является линейной комбинацией e 1, e 2, e 3, e 4: 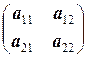 = a 11
= a 11 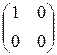 + a 12
+ a 12 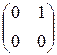 + a 21
+ a 21 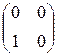 + a 22
+ a 22 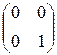 .
.
II. Система векторов
e 1=(1, 0, 0, …, 0),
e 2=(0, 1, 0, …, 0),
e 3=(0, 0, 1, …, 0), (3.2)
………………....,
en =(0, 0, 0, …, 1)
образует базис арифметического пространства An. При этом, если 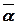 = (a 1, a 2, …, an)Î An, то
= (a 1, a 2, …, an)Î An, то 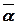 =a 1 e 1+ a 2 e 2+…+ anen, то есть α 1, α 2, …, αn – координаты вектора
=a 1 e 1+ a 2 e 2+…+ anen, то есть α 1, α 2, …, αn – координаты вектора 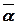 в базисе (е).
в базисе (е).
Действительно, во-первых, эта система векторов является линейно независимой: из a 1 e 1+ a 2 e 2+…+ anen =0 следует a 1= a 2=…= an =0, так как имеет место следующая цепочка равносильностей
a 1 e 1+ a 2 e 2+…+ anen = 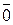 Û a 1(1, 0, …, 0)+ a 2(0, 1, …, 0)+…+ an (0, 0, …, 1)=(0, 0, …, 0)
Û a 1(1, 0, …, 0)+ a 2(0, 1, …, 0)+…+ an (0, 0, …, 1)=(0, 0, …, 0)
Û (a 1, 0, …, 0)+ (0, a 2, …, 0)+…+ (0, 0, …, an)=(0, 0, …, 0) Û
(a 1, a 2, …, an)=(0, 0, …, 0) Û a 1=0, a 2=0, …, an =0.
Во-вторых, если 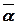 = (a 1, a 2, …, an)– произвольный вектор из An, то
= (a 1, a 2, …, an)– произвольный вектор из An, то
a 1 e 1+ a 2 e 2+…+ anen = a 1(1, 0, …, 0)+ a 2(0, 1, …, 0)+…+ an (0, 0, …, 1)=
=(a 1, a 2, …, an)= 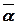 .
.
3.2.5. Определение. Базис, составленный из системы векторов (3.2) называется стандартным базисом арифметического линейного пространства.
3.3. Упражнение. Доказать, что векторы a 1, a 2, a 3 упражнения 2.3.2 образуют базис в A 3, и найти координаты вектора a 4 в этом базисе.
Решение. а) Согласно определения базиса покажем, что векторы a 1, a 2, a 3 линейно независимы и любой вектор x =(x 1, x 2, x 3)Î A 3 является их линейной комбинацией.
Составим для a 1, a 2, a 3 равенство a 1 a 1+ a 2 a 2+ a 3 a 3=0 V и подвергнем его равносильным преобразованиям:
|
|
|
a 1 a 1+ a 2 a 2+ a 3 a 3=0 V Û
Û a 1(1, 1, 1)+ a 2(0, 1, 1)+ a 3(0, 0, 1)=(0, 0, 0) Û
Û (a 1, a 1+ a 2, a 1+ a 2+ a 3)=(0, 0, 0) Û
Û 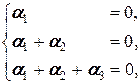 Û
Û 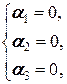
и векторы a 1, a 2, a 3 линейно независимы.
Теперь покажем, что существуют a 1, a 2, a 3 такие, что a 1 a 1+ a 2 a 2+ a 3 a 3= x, где x =(x 1, x 2, x 3)Î A 3. Действительно,
a 1 a 1+ a 2 a 2+ a 3 a 3= x Û (a 1, a 1+ a 2, a 1+ a 2+ a 3)=(x 1, x 2, x 3) Û 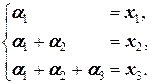
Так как определитель D= 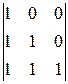 =0 системы не равен 0, то эта система - определённая, то есть для данных x 1, x 2, x 3 имеется единственное решение (a 1, a 2, a 3) этой системы, которое удовлетворяет равенству a 1 a 1+ a 2 a 2+ a 3 a 3= x. Это означает, что произвольный вектор x из A 3 является линейной комбинацией векторов a 1, a 2, a 3. Наконец, мы видели, что -3 a 1-3 a 2-3 a 3+ a 4=0 V, откуда a 4=3 a 1+3 a 2+3 a 3 (см. решение Упражнения 2.3.2 а)). Это означает, что (3, 3, 3) - координаты a 4 в базисе (a 1, a 2, a 3).
=0 системы не равен 0, то эта система - определённая, то есть для данных x 1, x 2, x 3 имеется единственное решение (a 1, a 2, a 3) этой системы, которое удовлетворяет равенству a 1 a 1+ a 2 a 2+ a 3 a 3= x. Это означает, что произвольный вектор x из A 3 является линейной комбинацией векторов a 1, a 2, a 3. Наконец, мы видели, что -3 a 1-3 a 2-3 a 3+ a 4=0 V, откуда a 4=3 a 1+3 a 2+3 a 3 (см. решение Упражнения 2.3.2 а)). Это означает, что (3, 3, 3) - координаты a 4 в базисе (a 1, a 2, a 3).
Ответ: а) (3, 3, 3) - координаты a 4 в базисе a 1, a 2, a 3.
 2015-03-08
2015-03-08 589
589








