Если каждому натуральному числу 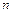 по некоторому правилу
по некоторому правилу 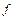 поставлено в соответствие одно вполне определённое действительное число
поставлено в соответствие одно вполне определённое действительное число 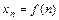 , то говорят, что задана числовая последовательность
, то говорят, что задана числовая последовательность 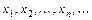 . Кратко обозначают
. Кратко обозначают 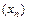 . Число
. Число 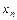 называется общим членом последовательности. Последовательность называют также функцией натурального аргумента. Последовательность всегда содержит бесконечно много элементов, среди которых могут быть равные.
называется общим членом последовательности. Последовательность называют также функцией натурального аргумента. Последовательность всегда содержит бесконечно много элементов, среди которых могут быть равные.
Число 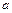 называется пределом последовательности
называется пределом последовательности 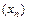 , и пишут
, и пишут 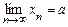 , если для любого числа
, если для любого числа 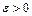 найдётся номер
найдётся номер 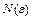 такой, что при всех
такой, что при всех 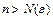 выполняется неравенство
выполняется неравенство 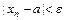 .
.
Последовательность 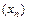 , имеющая конечный предел, называется сходящейся, в противном случае – расходящейся.
, имеющая конечный предел, называется сходящейся, в противном случае – расходящейся.
Последовательность 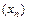 называется бесконечно малой, если
называется бесконечно малой, если 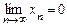 . Последовательность
. Последовательность 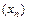 называется бесконечно большой (сходящейся к бесконечности) и пишут
называется бесконечно большой (сходящейся к бесконечности) и пишут 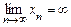 , если для любого числа
, если для любого числа 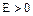 найдётся номер
найдётся номер 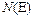 такой, что при всех
такой, что при всех 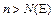 выполняется неравенство
выполняется неравенство 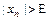 .
.
Число 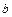 называется пределом функции
называется пределом функции 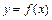 при
при 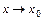 (или в точке
(или в точке 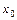 ), и пишут
), и пишут 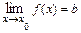 , если для любого числа
, если для любого числа 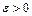 найдётся число
найдётся число 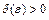 такое, что при всех
такое, что при всех 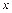 , удовлетворяющих условию
, удовлетворяющих условию 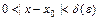 , выполняется неравенство
, выполняется неравенство 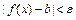 .
.
|
|
|
Число 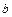 называется пределом функции
называется пределом функции 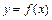 при
при 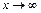 , и пишут
, и пишут 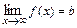 , если для любого числа
, если для любого числа 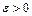 найдётся число
найдётся число 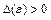 такое, что при всех
такое, что при всех 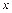 , удовлетворяющих условию
, удовлетворяющих условию 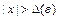 , выполняется неравенство
, выполняется неравенство 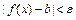 .
.
Рассматривают также односторонние пределы функций: 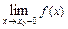 ,
, 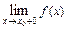 ,
, 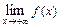 ,
, 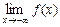 , где
, где 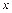 стремится к
стремится к 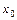 ,
, 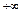 ,
, 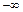 или только с левой стороны или только с правой стороны.
или только с левой стороны или только с правой стороны.
Основные утверждения, используемые для вычисления пределов функций при 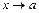 (в дальнейшем
(в дальнейшем 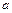 - или число
- или число 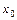 или символ
или символ 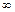 ):
):
1) Если 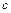 - постоянная величина, то
- постоянная величина, то 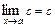 .
.
2) Если существуют конечные пределы 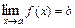 ,
, 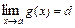 , то:
, то:
а) 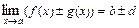 ; б)
; б) 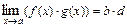 ;
;
в) 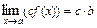
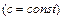 ; г)
; г) 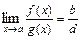 , если
, если 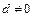 .
.
При вычислении пределов постоянно пользуются и тем, что для любой основной элементарной функции 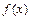 и точки
и точки 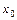 из её области определения справедливо соотношение
из её области определения справедливо соотношение 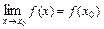 .
.
Функция 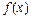 называется бесконечно большой при
называется бесконечно большой при 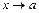 , если
, если 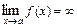 . Функция
. Функция 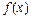 называется бесконечно малой при
называется бесконечно малой при 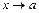 , если
, если 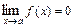 .
.
Основные утверждения для бесконечно больших функций, используемые для вычисления пределов при 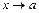 :
:
1) Если 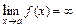 , то
, то 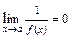 ,если
,если 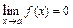 , то
, то 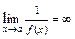
2) Если 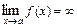 и
и 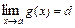 , то
, то 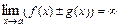 .
.
3) Если 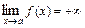 и
и 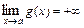 , то
, то 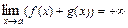 .
.
4) Если 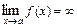 и
и 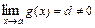 , то
, то 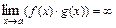 .
.
5) Если 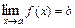 и
и 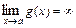 , то
, то 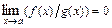 .
.
6) Если 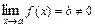 и
и 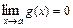 , то
, то 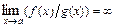 .
.
Если непосредственное применение свойств конечных пределов и бесконечно больших функций приводит к неопределённым выражениям, символически обозначаемым: 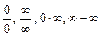 , то для вычисления предела – «раскрытия неопределённости» - преобразовывают выражение так, чтобы получить возможность его вычислить.
, то для вычисления предела – «раскрытия неопределённости» - преобразовывают выражение так, чтобы получить возможность его вычислить.
В задачах 4.85-4.88, используя определение предела, доказать, что 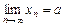 и найти номер
и найти номер 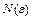 такой, что
такой, что 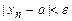 для всех
для всех 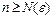 :
:
4.85 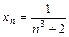 ,
, 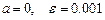 .
.
4.86 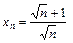 ,
, 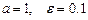 .
.
4.87 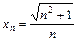 ,
, 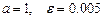 .
.
4.88 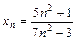 ,
, 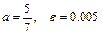 .
.
В задачах 4.89-4.111 найти пределы последовательностей:
4.89 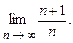 4.90
4.90 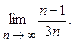 4.91
4.91 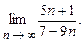
4.92 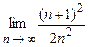 . 4.93
. 4.93 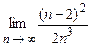 . 4.94
. 4.94 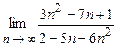 .
.
4.95 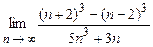 . 4.96
. 4.96 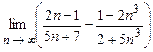 .
.
4.97 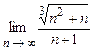 . 4.98
. 4.98 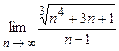 .
.
4.99 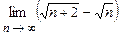 . 4.100
. 4.100 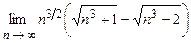 .
.
|
|
|
4.101 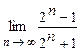 . 4.102
. 4.102 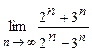 . 4.103
. 4.103 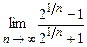 .
.
4.104 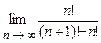 . 4.105
. 4.105 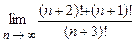 .
.
4.106 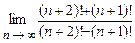 . 4.107
. 4.107 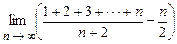 .
.
4.108 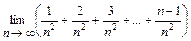 .
.
4.109 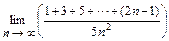 . 4.110
. 4.110 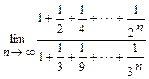 .
.
4.111 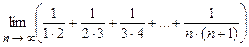 .
.
В задачах 4.112-4.113 пользуясь только определением предела функции доказать, что 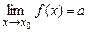 и заполнить таблицу:
и заполнить таблицу:
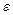
| 0.1 | 0.01 | 0.001 |
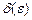
|
4.112 а) 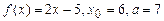 ; б)
; б) 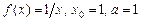 .
.
4.113 а) 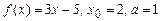 ; б)
; б) 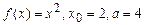 .
.
В задачах 4.114-4.132 вычислить пределы рациональных выражений:
4.114 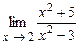 . 4.115
. 4.115 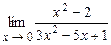 .
.
4.116 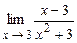 . 4.117
. 4.117 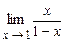 .
.
4.118 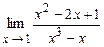 . 4.119
. 4.119 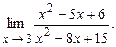
4.120 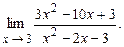 4.121
4.121 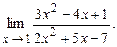
4.122 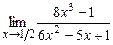 . 4.123
. 4.123 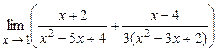 .
.
4.124 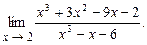 4.125
4.125 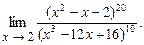
4.126 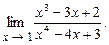 4.127
4.127 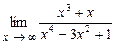 .
.
4.128 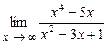 . 4.129
. 4.129 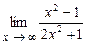 .
.
4.130 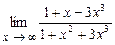 . 4.131
. 4.131 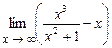 .
.
4.132 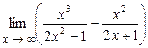 .
.
В задачах 4.133-4.149 вычислить пределы иррациональных выражений:
4.133 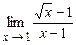 . 4.134
. 4.134 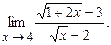
4.135 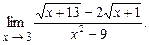 4.136
4.136 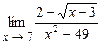 .
.
4.137 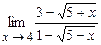 . 4.138
. 4.138 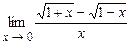 .
.
4.139 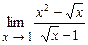 . 4.140
. 4.140 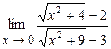 .
.
4.141 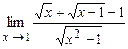 . 4.142
. 4.142 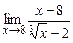 .
.
4.143 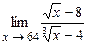 . 4.144
. 4.144 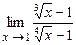 .
.
4.145 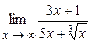 . 4.146
. 4.146 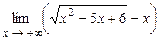 . 4.147
. 4.147 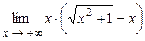 . 4.148
. 4.148 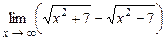 .
.
4.149 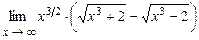 .
.
Первым замечательным пределом называется предел: 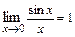 . Следствиями из него являются пределы:
. Следствиями из него являются пределы:
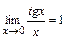 ,
, 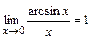 ,
, 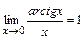 .
.
В задачах 4.150-4.170, используя 1-ый замечательный предел, вычислить пределы:
4.150 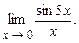 4.151
4.151 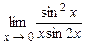 . 4.152
. 4.152 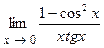 . 4.153
. 4.153 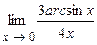 . 4.154
. 4.154 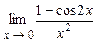 . 4.155
. 4.155 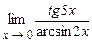 .
.
4.156 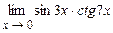 . 4.157
. 4.157 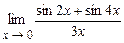 .
.
4.158 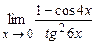 . 4.159
. 4.159 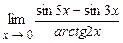 .
.
4.160 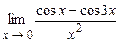 . 4.161
. 4.161 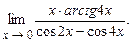
4.162 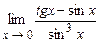 . 4.163
. 4.163 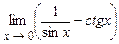 .
.
4.164 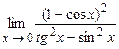 . 4.165
. 4.165 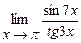 .
.
4.166. 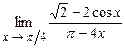 . 4.167.
. 4.167. 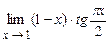 .
.
4.168 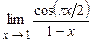 . 4.169
. 4.169 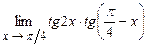 .
.
4.170 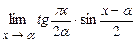 .
.
Вторым замечательным пределом называются пределы:
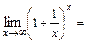
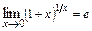 ,
,
где 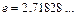 -основание натуральных логарифмов (число Непера). Он используется для вычисления предела степенно-показательной функции
-основание натуральных логарифмов (число Непера). Он используется для вычисления предела степенно-показательной функции 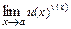 , где
, где 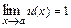 и
и 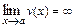 .
.
При нахождении пределов 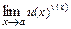 следует иметь в виду:
следует иметь в виду:
1) Если 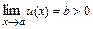 ,
, 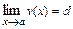 , то
, то 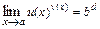 .
.
2) Если 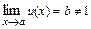 ,
, 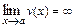 , то
, то 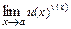 вычисляют, учитывая, что:
вычисляют, учитывая, что: 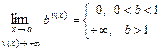 ,
, 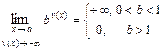 .
.
4.171 Доказать пределы:
а) 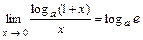 ; б)
; б) 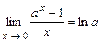 ; в)
; в) 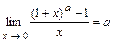
В задачах 4.172-4.174 вычислить пределы:
4.172 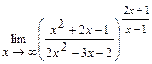 . 4.173
. 4.173 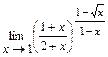 . 4.174
. 4.174 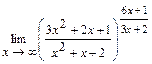 .
.
В задачах 4.175-4.204, используя 2-oй замечательный предел, а также результаты задачи 4.171, вычислить пределы:
4.175 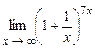 . 4.176
. 4.176 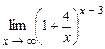 .
.
4.177 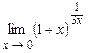 . 4.178
. 4.178 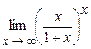 .
.
4.179 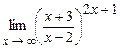 . 4.180
. 4.180 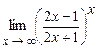 .
.
4.181 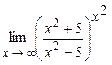 . 4.182
. 4.182 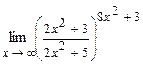 .
.
4.183 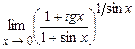 . 4.184
. 4.184 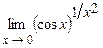 .
.
4.185 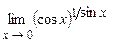 . 4.186
. 4.186 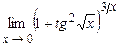 .
.
4.187 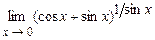 . 4.188
. 4.188 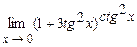 .
.
4.189 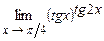 . 4.190
. 4.190 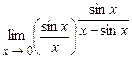 .
.
4.191 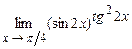 . 4.192
. 4.192 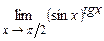
4.193 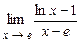 . 4.194
. 4.194 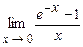 .
.
4.195 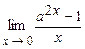 . 4.196
. 4.196 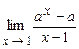 .
.
4.197 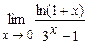 . 4.198
. 4.198 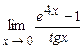 .
.
4.199 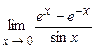 . 4.200
. 4.200 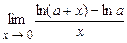 .
.
4.201 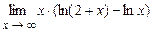 . 4.202
. 4.202 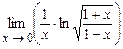 .
.
4.203 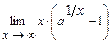 . 4.204
. 4.204 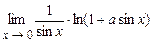 .
.
Бесконечно малые функции 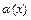 и
и 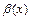 при
при 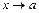 называются эквивалентными, и пишут
называются эквивалентными, и пишут 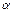 ~
~ 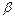 , если
, если 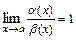 .
.
Принцип замены эквивалентных бесконечно малых функций, состоит в том, что при вычислении предела частного 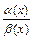 или произведения
или произведения 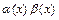 одну из функций (или обе) в этих выражениях можно заменить эквивалентной функцией. Так, если
одну из функций (или обе) в этих выражениях можно заменить эквивалентной функцией. Так, если 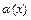 ~
~ 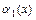 ,
, 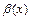 ~
~ 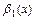 при
при 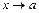 , то:
, то:
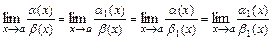 ;
;
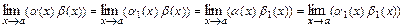
Основные эквивалентности при 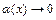
| |||
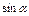 ~ ~ 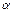
| 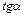 ~ ~ 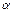
| 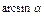 ~ ~ 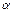
| 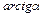 ~ ~ 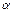
|
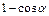 ~ ~ 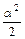
| 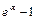 ~ ~ 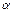
| 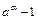 ~ ~ 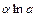
| 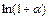 ~ ~ 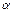
|
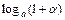 ~ ~ 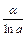
| 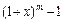 ~ ~ 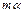
| 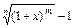 ~ ~ 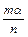
|
В задачах 4.205-4.222 вычислить пределы с помощью принципа замены эквивалентных бесконечно малых функций:
4.205. 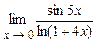 . 4.206
. 4.206 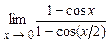 .
.
4.207 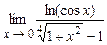 . 4.208
. 4.208 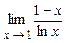 .
.
4.209 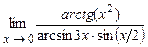 . 4.210
. 4.210 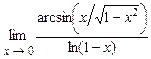 .
.
4.211 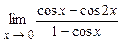 . 4.212
. 4.212 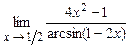 .
.
4.213 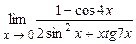 . 4.214
. 4.214 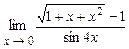 .
.
4.215 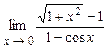 . 4.216
. 4.216 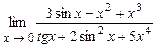 .
.
4.217 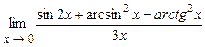 . 4.218
. 4.218 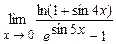 .
.
4.219 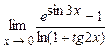 . 4.220
. 4.220 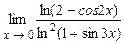 .
.
4.221 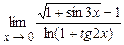 . 4.222
. 4.222 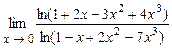 .
.
4.223 Доказать, что при 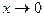
а) 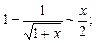 б)
б) 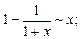 в)
в) 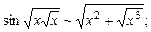
г) 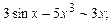 д)
д) 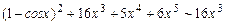 .
.
Если 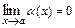 ,
, 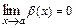 ,
, 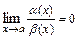 и при этом существует действительное число
и при этом существует действительное число 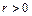 такое, что
такое, что 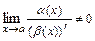 , то
, то 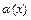 называется бесконечно малой функцией порядка
называется бесконечно малой функцией порядка 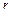 относительно
относительно 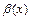 .
.
В задачах 4.224-4.235 определить порядок малости 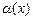 от-носительно
от-носительно 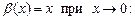
4.224 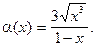 4.225
4.225 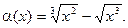
4.226  4.227
4.227 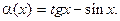
4.228 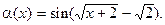 4.229
4.229 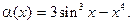
4.230 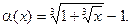 4.231
4.231 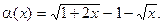
4.232 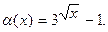 4.233
4.233 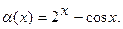
4.234 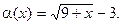 4.235
4.235 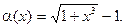
Если 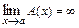 ,
, 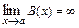 ,
, 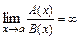 или
или 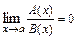 и при этом существует действительное число
и при этом существует действительное число 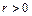 такое, что
такое, что 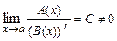 , (
, (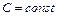 ), то
), то 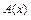 называется бесконечно большой функцией порядка
называется бесконечно большой функцией порядка 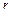 относительно
относительно 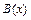 .
.
В задачах 4.236-4.241 определить порядок роста бесконечно большой функции 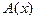 относительно
относительно 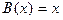 при
при 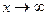 :
:
4.236 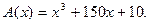 4.237
4.237 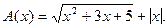
4.238 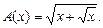 4.239
4.239 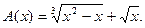
4.240 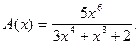 4.241
4.241 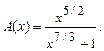
В задачах 4.242-4.247 найти односторонние пределы:
4.242 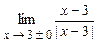 . 4.243
. 4.243 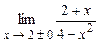 .
.
4.244 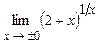 . 4.245
. 4.245 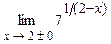 .
.
4.246 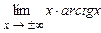 . 4.247
. 4.247 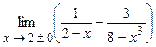 .
.
 2015-03-20
2015-03-20 856
856








