Частотные характеристики устойчивости

Позволяют достаточно наглядно провести анализ устойчивости либо по частотным характеристикам объектов и систем, либо по их частям.

Принцип аргумента. Запишем характеристическое уравнение в форме Безу:

a_n(p-p₁)… (p-p_n)=0

p_i-корни уравнения

p-некоторая переменная величина. (если записать решение однородного дифференциального уравнения в виде Ce^pt, подставить это решение в дифференциальное уравнение и разделить на Ce^pt-pⁿ)

Если заменить p на jω, то получим некоторую формулу:

D(jω)=a_n(jω-p₁)… (jω-p_n)

где p_i=α_i+jβ_i

Если рассмотреть отдельную каждую скобку, представив ее графически на комплексной плоскости, то каждая скобка изобразится в виде вектора.

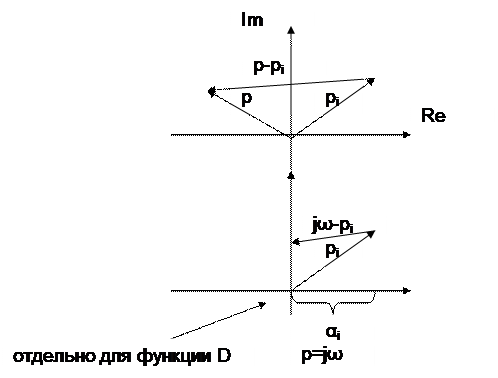
D(jω)=a_n(-α₁+j(ω-β)₁)…(-α_n+j(ω-β)_n)

Если ω изменяется от – ∞ до +∞ то вектор разности будет поворачиваться на угол π по часовой стрелке, если α>0 или против часовой стрелки если α<0.

Поскольку D(jω) можно представить как

D(jω)=A(ω)e^jγ(ω)

где

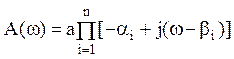
Поскольку D(jω) можно записать в виде представленном выше, то получается что фазовый угол равен сумме фазовых углов всех составляющих скобок при изменени ω от -∞ до +∞. Вектор D(jω) повернется на угол:

(n-m)π-mπ=(n-2m)π

где n – число правых корней, а поворот против

часовой стрелки считается положительным.

Если все корни левые и не нулевые, то угол составит π.

Функция D(jω), полученная заменой в характерном уравнении p на jω называется функцией Михайлова.