2015-03-07
739
Пусть имеется k реализаций (k ³10) случайного процесса X (t), и пусть измерения этого процесса производятся в моменты времени t 1, t 2, t 3, … tn, тогда оценка математического ожидания случайного процесса X (t) выражается формулой.
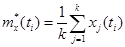(6.104)
Таким образом, для того чтобы получить оценку математического ожидания необходимо рассчитать среднее значение для каждого сечения.
Аналогичным образом, для того чтобы получить оценку дисперсии случайного процесса X (t) необходимо рассчитать оценку дисперсии для каждого сечения:
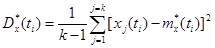. (6.105)
Оценка среднеквадратического отклонения случайного процесса X (t) равна:
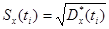. (6.106)
Оценка корреляционной функции случайного процесса X (t) в общем случае определяется выражением:
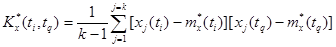. (6.107)
Заметим, что при i = q формула (6.107) превращается в формулу (6.105).
Оценка нормированной корреляционной функции случайного процесса X (t) определяется выражением:
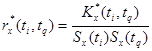(6.108)
Как следует из формулы (6.108) эмпирической оценкой нормированной корреляционной функции процесса X (t) будет корреляционная матрица вида:
|
|
|
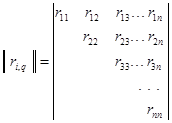, (6.109)
где ri,q – коэффициенты парной корреляции между сечениями; n – число сечений.
Для стационарного случайного процесса математическое ожидание, дисперсия и СКО являются константами и их можно оценить по любому сечению. Однако более надежный результат будет получен, если сначала рассчитать оценку искомой характеристики для каждого сечения, а затем найти ее среднее значение по всем сечениям.
Корреляционная функция стационарного процесса не зависит от того, для каких моментов времени рассматриваются сечения, а зависит только от расстояния между сечениями t. В этом случае оценка корреляционной функции записывается следующим образом:
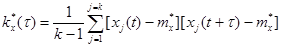. (6.110)
Оценка нормированной корреляционной функции стационарного процесса будет иметь вид:
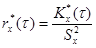. (6.111)
Напомним, что эту функцию обычно называют автокорреляционной функцией.
Из формул (6.110) и (6.111) видно, что, меняя t, можно получить несколько оценок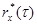 
для одного и того же t.
Наилучшей эмпирической оценкой нормированной корреляционной функции стационарного случайного процесса будет столбец парных коэффициентов корреляции полученный осреднением диагональных элементов матрицы (6.109):
;
;
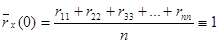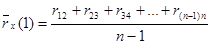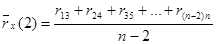и т. д.
Таким образом, если мы имеем дело с реализациями конечной длины то при увеличении t число коэффициентов парной корреляции, по которым производится осреднение, уменьшается, и точность оценки ординат корреляционной функции снижается.
Погрешность расчета выборочных ординат автокорреляционной функции стационарного случайного процесса в этом случае можно оценить по формуле
|
|
|
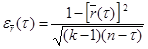, (6.112)
где k – количество реализаций (k ³ 10); n – длина реализаций (количество сечений); t – расстояние между сечениями (t < n).
