Пример 1. Составить уравнение плоскости 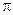 , проходящей через заданную точку
, проходящей через заданную точку 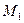 (2,1,-1) и параллельной плоскости
(2,1,-1) и параллельной плоскости 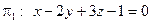 .
.
Решение. Нормаль к плоскости 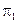 :
: 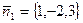 . Поскольку плоскости параллельны, то нормаль
. Поскольку плоскости параллельны, то нормаль 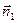 является и нормалью к искомой плоскости
является и нормалью к искомой плоскости  . Используя уравнение плоскости, проходящей через заданную точку (3), получим для плоскости
. Используя уравнение плоскости, проходящей через заданную точку (3), получим для плоскости  уравнение:
уравнение:
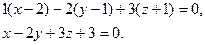
Ответ: 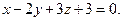
Пример 2. Основанием перпендикуляра, опущенного из начала координат на плоскость  , является точка
, является точка 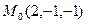 . Найти уравнение плоскости
. Найти уравнение плоскости 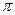 .
.
Решение. Вектор 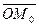 является нормалью к плоскости
является нормалью к плоскости 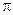 . Точка М0 принадлежит плоскости. Можно воспользоваться уравнением плоскости, проходящей через заданную точку (3):
. Точка М0 принадлежит плоскости. Можно воспользоваться уравнением плоскости, проходящей через заданную точку (3):
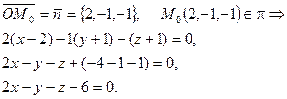
Ответ: 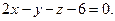
Пример 3. Построить плоскость  , проходящую через точки
, проходящую через точки 
 и перпендикулярную плоскости
и перпендикулярную плоскости 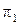 :
: 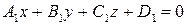 .
.
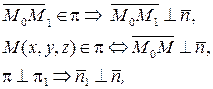
Следовательно, чтобы некоторая точка М (x, y, z) принадлежала плоскости 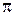 , необходимо, чтобы три вектора
, необходимо, чтобы три вектора 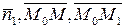 были компланарны:
были компланарны:
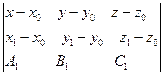 =0.
=0.
Осталось раскрыть определитель и привести полученное выражение к виду общего уравнения (1).
Пример 4. Плоскость  задана общим уравнением:
задана общим уравнением:
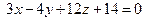 .
.
Найти отклонение точки 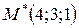 от заданной плоскости.
от заданной плоскости.
Решение. Приведем уравнение плоскости к нормальному виду.
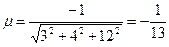 ,
,
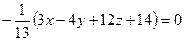 .
.
Подставим в полученное нормальное уравнение координаты точки М*.
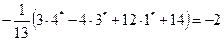 .
.
Ответ: 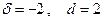 .
.
Пример 5. Пересекает ли плоскость 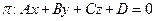 отрезок
отрезок 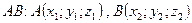 .
.
Решение. Чтобы отрезок АВ пересекал плоскость, отклонения 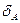 и
и 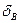 от плоскости
от плоскости 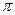 должны иметь разные знаки:
должны иметь разные знаки:
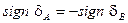 .
.
Пример 6. Пересечение трех плоскостей в одной точке.
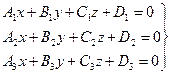
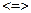
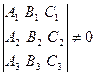 .
.
Система имеет единственное решение, следовательно, три плоскости имеют одну общую точку.
Пример 7. Нахождение биссектрис двугранного угла, образованного двумя заданными плоскостями.
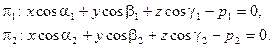
Пусть 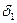 и
и 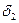 - отклонение некоторой точки
- отклонение некоторой точки 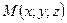 от первой и второй плоскостей.
от первой и второй плоскостей.
На одной из биссектральных плоскостей (отвечающей тому углу, в котором лежит начало координат) эти отклонения равны по модулю и знаку, а на другой – равны по модулю и противоположны по знаку.
1) 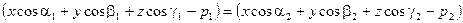
- это уравнение первой биссектральной плоскости.
2) 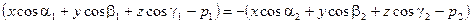
- это уравнение второй биссектральной плоскости.
Пример 8. Определение местоположения двух данных точек 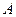 и
и 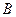 относительно двугранных углов, образованных данными плоскостями.
относительно двугранных углов, образованных данными плоскостями.
Пусть 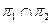 . Определить: в одном, в смежных или в вертикальных углах находятся точки
. Определить: в одном, в смежных или в вертикальных углах находятся точки 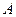 и
и 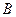 .
.
1) Находим 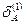 и
и 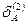 ,
, 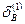 и
и 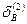 - это отклонения точек А и В от плоскостей
- это отклонения точек А и В от плоскостей 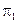 и
и 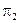 .
.
а). Если 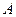 и
и 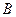 лежат по одну сторону от
лежат по одну сторону от 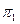 и от
и от 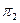 , то они лежат в одном двугранном углу.
, то они лежат в одном двугранном углу.
б). Если 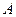 и
и 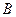 лежат по одну сторону от
лежат по одну сторону от 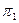 и по разные от
и по разные от 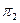 , то они лежат в смежных углах.
, то они лежат в смежных углах.
в). Если 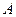 и
и 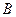 лежат по разные стороны от
лежат по разные стороны от 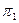 и
и 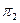 , то они лежат в вертикальных углах.
, то они лежат в вертикальных углах.
Линии в пространстве. Прямая в пространстве. 2
Канонические уравнения прямой в пространстве. 3
Параметрические уравнения прямой. 4
Уравнения прямой, проходящей через две заданные точки. 4
Угол между двумя прямыми в пространстве. 5
Угол между прямой и плоскостью.. 5
Условие принадлежности двух прямых одной плоскости. 6
Некоторые задачи на построение прямых и плоскостей. 6
Примеры решения задач по теме «Аналитическая геометрия». 11
Линии в пространстве. Прямая в пространстве
В аналитической геометрии каждая линия рассматривается как пересечение двух поверхностей и соответственно определяется заданием двух уравнений.
Пусть F1 (x, y, z)=0 и F 2(x, y, z)=0 – уравнения двух поверхностей.
Система уравнений 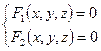 определяет линию, являющуюся их пересечением.
определяет линию, являющуюся их пересечением.
Следовательно, прямую 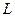 можно задать системой двух уравнений плоскостей:
можно задать системой двух уравнений плоскостей:
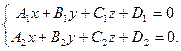 (1)
(1)
Это возможно только в том случае, когда плоскости не совпадают и не параллельны, т.е. когда нормали 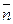 1=
1= 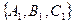 и
и 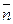 2=
2= 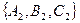 не коллинеарны.
не коллинеарны.
Система (1) – это общее уравнение прямой в пространстве.
Через каждую прямую проходит бесконечное множество плоскостей (пучок плоскостей).
Определение. Cовокупность всех плоскостей, проходящих через одну и ту же прямую L, называется пучком плоскостей с центром в L.
Умножим уравнения системы (1) соответственно на коэффициенты 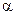 и
и 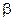 , одновременно не равные нулю.
, одновременно не равные нулю.
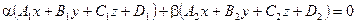 – уравнение плоскости, проходящей через прямую L.
– уравнение плоскости, проходящей через прямую L.
(Докажите самостоятельно аналогично доказательству для пучка прямых)
Определение. Совокупность всех плоскостей, проходящих через данную точку 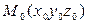 , называется связкой плоскостей с центром в точке M0.
, называется связкой плоскостей с центром в точке M0.
 2015-04-12
2015-04-12 3192
3192








