Кривая разгона является одной из основных динамических характеристик систем управления. Уравнение кривой разгона может быть получено экспериментальным путем (если это не противоречит функционированию исследуемого объекта) или путем решения дифференциального уравнения, которое описывает динамику объекта.
Поведение систем автоматического регулирования (САР) в процессе функционирования представляет собой сочетание статических и динамических режимов. Для проведения теоретических исследований САР и её отдельных элементов необходимо иметь уравнения, описывающие их поведение при изменяющихся внешних воздействиях. Эти уравнения представляют собой выраженные в математической форме соотношения, связывающие входные и выходные сигналы и воздействия.
В общем случае действие непрерывной линейной САР описывается неоднородным дифференциальным уравнением следующего вида:
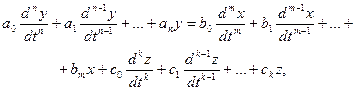
где a, b, c – постоянные коэффициенты, зависящие от параметров системы.
Решение неоднородных дифференциальных уравнений складывается из решения однородного дифференциального уравнения y о и частного решения y ч: 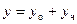 .
.
Для решения однородного дифференциального уравнения составляется характеристическое уравнение, и находятся его корни, далее, в зависимости от полученных значений (см. приложения, табл. 1.2) записывается общее решение. Частное решение получается в результате решения правой части дифференциального уравнения методом неопределенных коэффициентов.
В теории автоматического регулирования широко используется специальный метод прикладного анализа, в основе которого лежит функциональное преобразование Лапласа. Преобразование Лапласа служит для перехода от функции вещественного переменного – время, к функции комплексного переменного.
Преобразованной по Лапласу функцией называется функция комплексного переменного, определяемого соотношением:
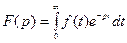 ,
,
где f (t) – исходная функция действительного переменного t, называемая оригиналом; р – комплексная переменная, 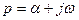 ; a, w – действительные переменные;
; a, w – действительные переменные; 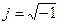 ; F (p) – функция комплексного переменного, называемая изображением по Лапласу функции f (t).
; F (p) – функция комплексного переменного, называемая изображением по Лапласу функции f (t).
Иначе это можно записать в виде: L { f (t)} = F (р), где L – символ преобразования Лапласа.
Обратный переход от изображения к оригиналу осуществляется по формуле 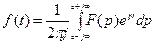 ,
,
где с – абсцисса сходимости функции f (t).
Использование преобразования Лапласа объясняется рядом преимуществ этого метода перед прямым решением задач в области действительного переменного. В частности, изображения некоторых функций оказываются проще их оригиналов.
Для нахождения изображения от производных используют правило дифференцирования: операция дифференцирования функции вещественного переменного соответствует операция умножения изображения функции на комплексную переменную в соответствующей степени.
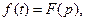
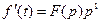 ,
,
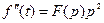 ,
,
……….,
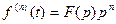 .
.
Использование преобразования Лапласа для решения дифференциальных уравнений, упрощает решение, благодаря тому, что в области комплексного переменного дифференциальное уравнение преобразуется в алгебраическое, а оригиналы найденного решения легко определяются по таблицам (см. приложения, табл. 1.3).
Решение дифференциального уравнения с применением преобразования Лапласа складывается из трех этапов:
1) преобразование уравнения по Лапласу с использованием правила дифференцирования;
2) отыскание решения в области комплексного переменного;
3) переход в область действительного переменного путем обратного преобразования по Лапласу функции и отыскание ее оригинала.
Пример 1. Решить неоднородное дифференциальное уравнение первого порядка 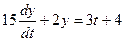 , с начальным условием:
, с начальным условием: 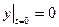 .
.
Алгоритм аналитического решения
1. Запишем однородное дифференциальное уравнение 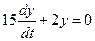 .
.
2. Заменим 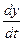 и y соответственно на k 1, k 0 = 1 и составим характеристическое уравнение
и y соответственно на k 1, k 0 = 1 и составим характеристическое уравнение  .
.
3. Корень характеристического уравнения 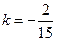 .
.
4. Общее решение дифференциального уравнения запишется в виде: 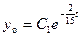 .
.
5. Правая часть уравнения представляет собой линейную зависимость, которую можно записать следующим образом: 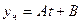 , откуда
, откуда 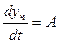 .
.
6. Подставим полученные значения в исходное уравнение: 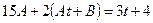 , откуда
, откуда 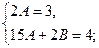 и
и 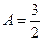 ,
, 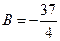 .
.
7. Запишем частное решение дифференциального уравнения: 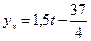 .
.
8. Решение исходного дифференциального уравнения: 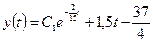 .
.
9. В полученное уравнение подставим начальное условие: 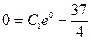 , откуда
, откуда 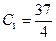 .
.
10. В результате уравнение будет иметь вид: 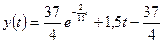 .
.
Алгоритм метода преобразования Лапласа
1. Преобразуем по Лапласу левую и правую части уравнения с учетом линейности этой операции, правил преобразования производных и изображения единичной функции, получим:
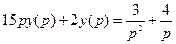 .
.
2. Решение этого уравнения: 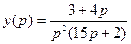 .
.
3. Раскладываем полученное уравнение на простейшие дроби:
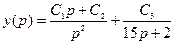 ,
,
откуда 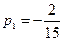 , p 2 = p 3 = 0. Постоянные С 1, С 2, С 3 находятся методом неопределенных коэффициентов из уравнений:
, p 2 = p 3 = 0. Постоянные С 1, С 2, С 3 находятся методом неопределенных коэффициентов из уравнений:
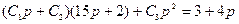 ,
,
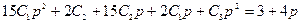 ,
,
откуда 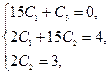
следовательно 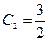 ,
, 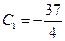 ,
, 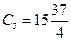 .
.
4. Подставляя вычисленные значения, получим:
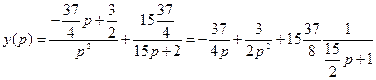 .
.
5. По табл. 1.3 производим обратное преобразование Лапласа и находим оригинал
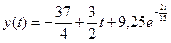 .
.
Получили аналогичное аналитическому решению выражение.
Пример 2. Решить неоднородное дифференциальное уравнение второго порядка 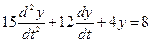 , с начальными условиями:
, с начальными условиями: 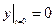 ,
, 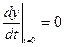 .
.
Алгоритм аналитического решения
1. Запишем однородное дифференциальное уравнение 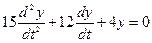 .
.
2. Заменим 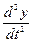 ,
, 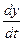 и y соответственно на k 2, k 1, k 0 = 1 и составим характеристическое уравнение
и y соответственно на k 2, k 1, k 0 = 1 и составим характеристическое уравнение 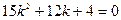 .
.
3. Найдем корни характеристического уравнения 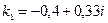 ,
, 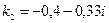 .
.
4. Общее решение дифференциального уравнения запишется в виде 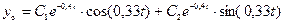 .
.
5. Правая часть уравнения представляет собой постоянную, частное решение можно записать следующим образом 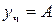 , откуда
, откуда 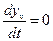 ,
, 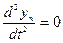 .
.
6. Подставим полученные значения в исходное уравнение: 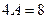 , откуда
, откуда 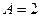 .
.
7. Запишем частное решение дифференциального уравнения 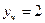 .
.
8. Решение исходного дифференциального уравнения 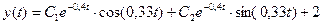 .
.
9. Для определения постоянных C 1 и C 2 запишем первую производную от полученной зависимости и подставим в уравнения соответствующие начальные условия.
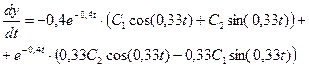
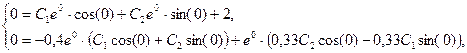
откуда, 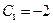 ,
, 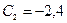 .
.
10. В результате уравнение будет иметь вид: 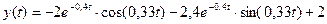 .
.
10. График решения при t, изменяющемся от 0 до 16 с шагом 1, представлен на рис. 1.
Алгоритм метода преобразования Лапласа
1. Преобразуем по Лапласу левую и правую части уравнения с учетом линейности этой операции, правил преобразования производных и изображения единичной функции, получим:
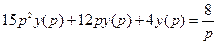 .
.
2. Решение этого уравнения: 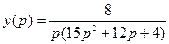 .
.
3. Преобразуем полученное уравнение к виду 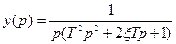 :
: 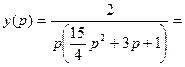
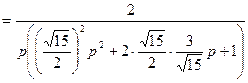 , т.е.
, т.е. 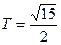 ,
, 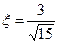 .
.
4. По табл. 1.3 производим обратное преобразование Лапласа при
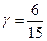 ,
, 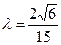 ,
, 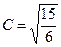 ,
, 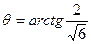 оригинал функции:
оригинал функции:
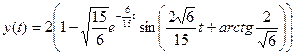 .
.
5. График y(t) при t =[0; 16] с шагом 1 на рис. 1.
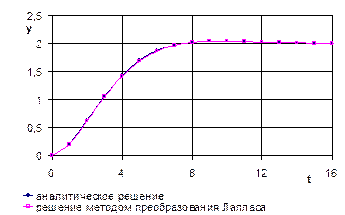
Рис. 1. График решения дифференциального уравнения 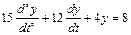 ,
, 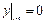 ,
, 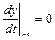 .
.
Контрольные вопросы
1. Что такое кривая разгона? Каким образом может быть получено уравнение кривой разгона?
2. Какого вида уравнениями описывается поведение САР в процессе функционирования?
3. Каковы этапы аналитического решения неоднородных дифференциальных уравнений?
4. Для чего служит преобразование Лапласа?
5. Как записываются формулы перехода от оригинала к изображению по Лапласу и обратно?
6. Каковы этапы решения дифференциальных уравнений с применением преобразования Лапласа?
 2015-04-12
2015-04-12 550
550








