Для натуральной системы координат.
При построении пространственной системы координат, связанной с кривой, за начало координат берут любую точку на кривой, а за оси ДПСК следующие: за ось абсцисс принимают касательную в этой точке, за ось ординат – главную нормаль, а за ось аппликат – бинормаль. За координатные плоскости выбирают: соприкасающуюся, нормальную и спрямляющую плоскости.
| b |
| P |
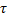 |
| n |
| норм |
| сопр |
| спрямл |
Способы задания пространственных кривых:
| Способ задания | Кривая |
| Векторно-параметрический | 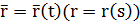 |
| Параметрический | 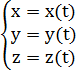 |
| Явный | 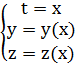 |
| Как пересечение 2-х поверхностей | 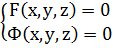 |
1) Касательная к пространственной кривой:
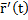 |
| R(t) |
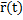 |
| O |
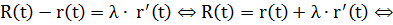
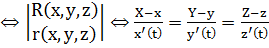
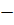 каноническое уравнение касательной
каноническое уравнение касательной
Получим уравнение касательной и кривой как пересечение поверхностей:
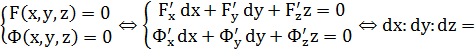
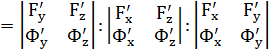 .
.
Тогда заменяя производные дифференциалами в уравнении касательной, получим:
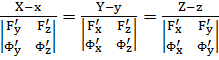 .
.
2) Нормальная плоскость и её уравнение:
| R |
| O |
 |
| r |
Def. Множество нормалей, проведенных к данной точке на кривой, образуют нормальную плоскость.
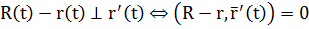 (векторное уравнение плоскости)
(векторное уравнение плоскости)
или если 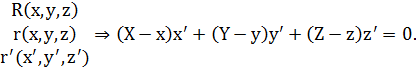
В случае, когда кривая задана неявно как пересечение двух плоскостей, уравнение нормальной плоскости следующее:
| N |
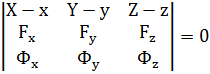 .
. 3) Соприкасающаяся плоскость
| R(t) |
| L |
 |
 |
| r(t) |
Рассмотрим дважды непрерывно дифференцируемую кривую L и т.  . В точке М определены векторы
. В точке М определены векторы 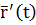 - вектор касательной и
- вектор касательной и 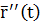 - вектор …. Если они не коллинеарны, то они и определены уравнениями соприкасающейся плоскости:
- вектор …. Если они не коллинеарны, то они и определены уравнениями соприкасающейся плоскости:
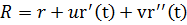 или
или 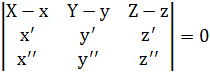 .
.
| b |
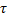 |
| n |
2. Уравнение нормальной плоскости
| R(t) |
| R(t) |
| R(t) |
| r(t) |
| n |
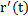 |
| b |
| норм |
Def. Множество всех нормалей проведенных к пространственной кривой в рассматриваемой точке и образуют нормальную плоскость.
Замечание. В качестве вектора нормали выбирают вектор касательной кривой, т.е. вектор 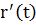 , тогда:
, тогда:
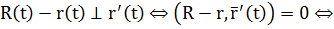
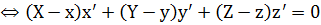 - уравнение нормальной плоскости
- уравнение нормальной плоскости
Если кривая задана неявно (как пересечение поверхностей 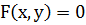 и
и 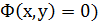 , то вектор
, то вектор 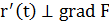 и
и 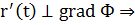 вектора
вектора  - компланарные
- компланарные 
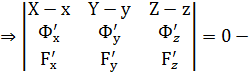 уравнение нормальной плоскости.
уравнение нормальной плоскости.
3. Соприкасающаяся плоскость криво
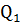 |
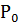 |
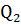 |
| ℒ |
Пусть т. 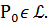 возьмем на ней еще точки
возьмем на ней еще точки 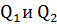 расположенные по разные стороны от т.
расположенные по разные стороны от т. 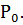 проведем через них плоскость.
проведем через них плоскость.
Def. Предельное положение построенной плоскости, проходящей через т. 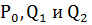 когда две из них
когда две из них 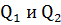 стремятся к третьей т.
стремятся к третьей т. 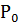 , и будем называть соприкасающейся плоскостью кривой в т.
, и будем называть соприкасающейся плоскостью кривой в т. 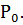
Теорема. Пусть r = r(t) – дважды непрерывно дифференцируемая кривая. Если в т. 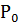 вектора
вектора 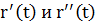 - неколлинеарны (
- неколлинеарны (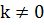 ), то в этой точке существует соприкасающаяся плоскость, и она проходит через вектора
), то в этой точке существует соприкасающаяся плоскость, и она проходит через вектора 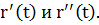
Замечание 1. Точки кривой, в которых векторы 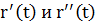 - коллинеарны, называются точками распрямления кривой.
- коллинеарны, называются точками распрямления кривой.
Замечание 2. Вектор нормали, лежащий в соприкасающейся плоскости, называется главным вектором нормали кривой. Орт этого вектора
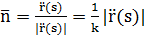 .
.
Замечание 3. Из теоремы следует, что вектора 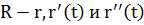 - коллинеарные, поэтому
- коллинеарные, поэтому
1) 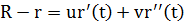 или
или 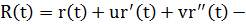 векторное уравнение плоскости или
векторное уравнение плоскости или
2) 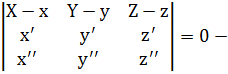 уравнение соприкасаящейся плоскости в координатном виде.
уравнение соприкасаящейся плоскости в координатном виде.
Так как 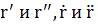 принадлежат соприкасающейся плоскости, то соприкасающуюся плоскость назавают плоскостью ускорения:
принадлежат соприкасающейся плоскости, то соприкасающуюся плоскость назавают плоскостью ускорения:
а) вектора 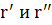 принадлежат соприкасающейся плоскости, т.к. плоскость проходит через касательную прямую;
принадлежат соприкасающейся плоскости, т.к. плоскость проходит через касательную прямую;
б) 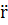 принадлежит соприкасающейся плоскости, т.е. плоскость проходит через главный вектор нормали;
принадлежит соприкасающейся плоскости, т.е. плоскость проходит через главный вектор нормали;
в) 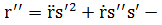 т.е. по нормале разложения вектора
т.е. по нормале разложения вектора 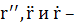 лежат в одной плоскости.
лежат в одной плоскости.
 2015-04-12
2015-04-12 1854
1854








