Любая АСР – совокупность звеньев. Модель системы – совокупность моделей ее элементов. Отсюда следует, что порядок уравнения системы n может быть достаточно большим. В случае n > 3 получить аналитические (общего вида) решения дифференциальных уравнений невозможно. Вместе с тем при n=3 решение получается громоздким и малообозримым.
Пользуясь численными методами, результаты для n > 3 получают лишь при конкретных значениях коэффициентов уравнений. Поэтому при расчете АСР, при выборе параметров элементов системы, сводящемуся к выбору коэффициентов ее дифференциального уравнения, приходиться производить многократные вычисления, т.е. использовать метод проб и ошибок. В процессе вычислений необходимо, варьируя коэффициентами, оценивать их влияние на переходные процессы в АСР и подбирать численные значения коэффициентов, при которых качество регулирования соответствовало бы желаемому. При больших n рассматривается задача становится трудоемкой и часто малоэффективной. Не случайно метод проб и ошибок называют в обиходе «методом тыка» (а вдруг попадешь).
Один из возможных путей исследования систем заключается в использовании метода разложения сложного на составляющие его простые части. Этот метод уже был использован при представлении сложных сигналов через сумму типовых воздействий. Другой пример – разложение функций в ряды, когда, по словам Лагранжа, «природа функций познается гораздо легче». Форма представления сложного через простые части по его же словам «кажется наиболее удобной для восприятия разума природных свойств» многих сложных явлений. Являясь общечеловеческим методом познания, данный метод в ряде случаев становиться единственным, позволяющим получить хоть какую - то информацию об изучаемом объекте. При исследовании АСР использование этого метода позволяет переходить от знания свойств элементов к пониманию свойств всей системы, а анализ влияния отдельных элементов на работу АСР дает возможность решать задачи выбора элементов и их параметров, при которых выполняются требования к качеству работы проектируемой системы.
Простыми частями, на основе которых могут быть сделаны заключения о динамических свойствах систем и сложных в динамическом отношении звеньев, являются так называемые типовые звенья. Типовые звенья описываются хорошо изученными дифференциальными уравнениями не выше второго порядка, число которых ограничено. Таким образом, типовые звенья – это известное ограниченное число простых динамических элементов, на основании которых может быть составлено представление о динамике любой сложной системы.
Как уже отмечалось, для эффективного решения задач теории автоматического управления, пользуются методом аналогии. Он позволяет свести изучение различных по физической природе, конструктивному выполнению, назначению и т.д. систем к исследованию одной обобщенной абстрактной математической модели системы. Данный подход находит отражение и при введении понятия «типовое звено». Любое типовое звено представляет также обобщенную абстрактную модель в виде дифференциального уравнения не выше второго порядка. Зная количественные характеристики типового звена, можно делать заключение о динамике любых реальных звеньев, имеющих аналогичный типовому звену вид управления. При этом нет необходимости выполнять никакие дополнительные расчеты. Достаточно приписать входному и выходному сигналам, а также коэффициентам передачи конкретные физические размерности и воспользоваться результатами исследования соответствующей абстрактной модели.
Типовые звенья делятся на позиционные, интегрирующие, дифференцирующие, запаздывания в соответствии со структурой их уравнений.
Позиционные звенья в правой части уравнения имеют только член, содержащий отклонение входной величины, а в левой части обязательно присутствует член, содержащий отклонение выходной величины
К позиционным относятся:
идеальное (безынерционное, усилительное) звено с уравнением, передаточной W(p) и переходной функциями h(t), график которой показан ниже
у(t) = k х (t) (16.1)
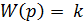
h(t)
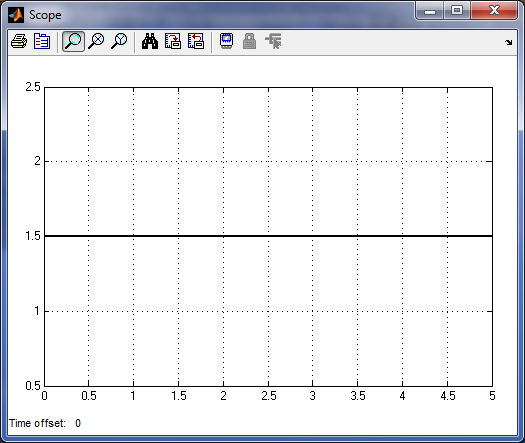 t
t
апериодическое звено 1-го порядка
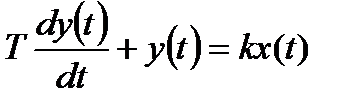 (16.2)
(16.2)
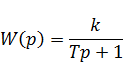
h(t)
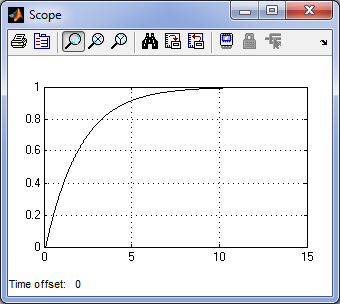 t
t
апериодическое звено 2-го порядка
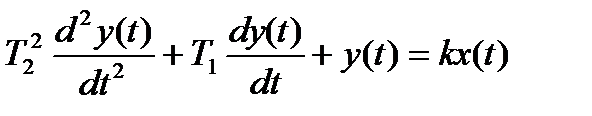 (16.3)
(16.3)
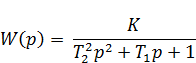
h(t)
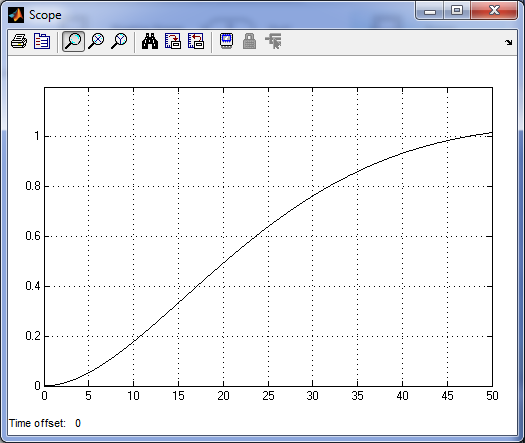 t
t
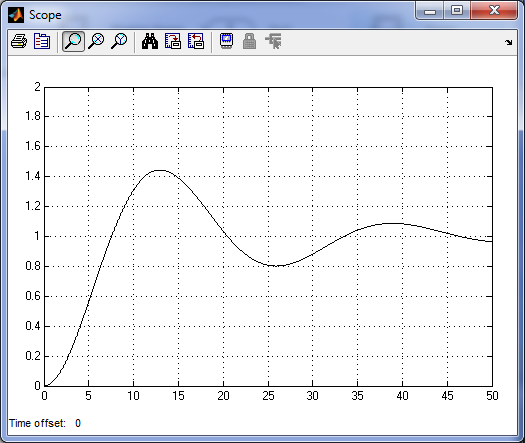
колебательное звено
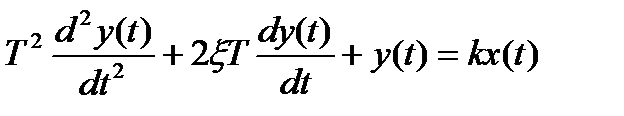 (16.4)
(16.4)
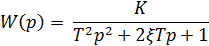
h(t)
 t
t
Здесь y(t) и x(t) - соответственно выходной и входной сигналы звеньев; Т, Т1, Т2 – постоянные времени; k – коэффициент передачи; ξ - параметр затухания
Апериодическое 2-го порядка и колебательное звенья имеют один и тот же порядок уравнения, однако корни характеристического уравнения, у первого - вещественные, а у второго комплексные. В связи с этим переходная функция 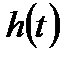 у первого - апериодическая (без колебаний), а у второго – имеет колебательный характер. После окончания переходных процессов
у первого - апериодическая (без колебаний), а у второго – имеет колебательный характер. После окончания переходных процессов
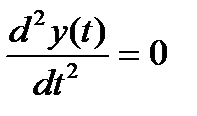 ;
; 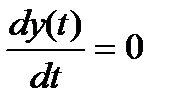 (16.5)
(16.5)
и все позиционные звенья имеют уравнение, как у без инерционного звена (16.1), т.е. в установившемся режиме определенному значению x соответствует определенное значение (позиция) y. Отсюда и их название – позиционные звенья.
Позиционные звенья являются статическими по входной величине. Как следует из графиков на рис.24, а, выходной сигнал У(t) всех звеньев за исключением идеального, отстает от изменения входного сигнала x(t). Для апериодического звена это отставание связано с постоянной времени Т, для апериодического звена 2-го порядка и для колебательного звена - с отношением Т1/Т2. Таким образом, Т, Т1 и Т2 характеризуют инерционность или инерционное запаздывание указанных звеньев.
Понятие «безынерционное звено» условно. В мире, где мы живем даже атом обладает массой и следовательно инерционен. В системах, состоящих из различных по динамическим, т.е. проявляющим себя во времени, в процессе, свойствам элементов, один из элементов, чаще всего это объект регулирования, гораздо инерционее других.
Это значит, что процессы в нем происходят, например, за минуты, а в других элементах – за секунды. Например, бак для нагрева в нем воды до определенной температуры гораздо инерционее электронного усилителя, используемого в системе для усиления электрических сигналов с датчика температуры. При математическом описании этих элементов в виде уравнения (16.2) постоянная времени T у бака будет в сотни раз больше, чем у усилителя. В этом случае, с практической точки зрения, усилитель можно считать безынерционным звеном системы.
К интегрирующим относятся звенья, выходной сигнал которых получается интегрированием входного сигнала.
Идеальное интегрирующее звено имеет уравнение
Y(t)= k 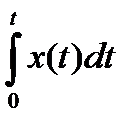 . (16.6)
. (16.6)
Продифференцировав левую и правую части уравнения (16.6), получим другую стандартную форму записи для интегрирующего звена:
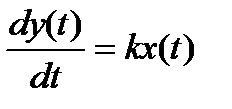 (16.7)
(16.7)
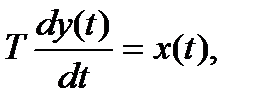 где T=
где T= 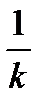 ,
,
k – коэффициент передачи по скорости
Передаточная и переходная функции данного звена будут
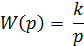
h(t)
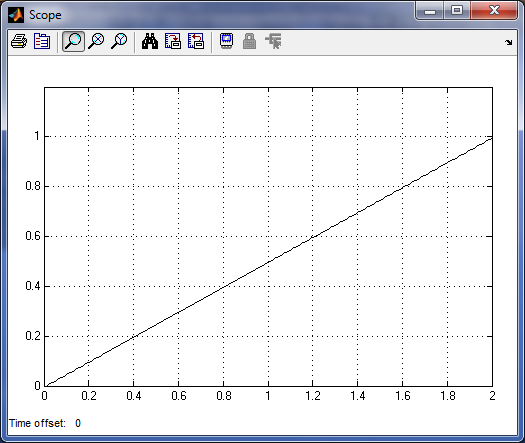 t
t
Инерционное интегрирующее звено имеет уравнение
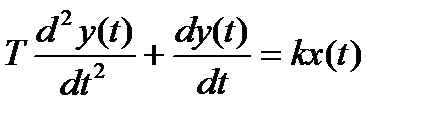 (16.8)
(16.8)
Передаточная и переходная функции данного звена будут
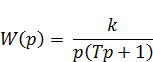
h(t)
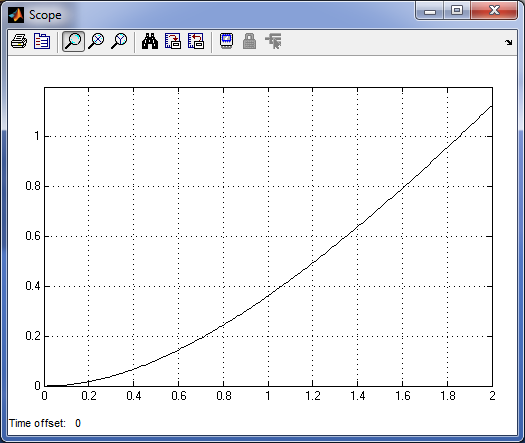 t
t
Дифференцирующие звенья – звенья, дифференцирующие входной сигнал. Иначе, выходной сигнал дифференцирующих звеньев содержит информацию о скорости изменения входного сигнала.
Идеальное дифференцирующее звено описывается уравнением
Y(t) = k 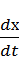 ,(16. 9)
,(16. 9)
а дифференцирующее звено, при необходимости учитывать его инерционность, уравнением
T 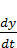 + y(t) = k
+ y(t) = k 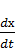 (16.10)
(16.10)
Передаточные функции данных звеньев соответственно равны
W(p) = kp и W(p) =  .
.
 2015-04-17
2015-04-17 1441
1441








