Первое достаточное условие экстремума

g Пусть функция дифференцируема в некоторой d-окрестности точки x ₀ за исключением, быть может, самой точки x ₀ (в самой точке x ₀ она предполагается, как минимум – непрерывной). Если f¢ (x) > 0 " x Î(x ₀ – d; x ₀) и f¢ (x) < 0 " x Î(x ₀; x ₀ + d), то есть производная меняет знак с плюса на минус при переходе через точку x ₀, то в точке x ₀ функция имеет локальный максимум. Если производная меняет знак с минуса на плюс,– то минимум. Если же производная при переходе через точку x ₀ знака не меняет, то в точке x ₀ функция экстремума не имеет.

4Рассмотрим случай, когда при переходе через точку x ₀ производная меняет знак с плюса на минус. Выберем произвольно x Î(x ₀ – d; x ₀). Применим формулу Лагранжа (6.2) к функции f (x) на промежутке [ x; x ₀]:

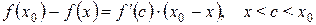. (6.3)

Так как по условию f¢ (x) > 0 " x Î(x ₀ – d; x ₀), то f¢ (с) > 0, кроме того, x ₀ – x > 0. Из формулы (6.3) видно, что f (x ₀) – f (x) > 0 или f (x ₀) > f (x).

Выберем теперь произвольную точку x Î(x ₀; x ₀ + d) и применим формулу Лагранжа к функции f (x) на промежутке [ x ₀; x ]:

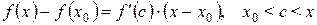. (6.4)

По условию на интервале (x ₀; x + δ) f¢ (x) < 0 и, следовательно, f¢ (с) < 0. Кроме того, x – x ₀ > 0. Из формулы (6.4) следует, что f (x) – f (x ₀) < 0 или, как и в предыдущем случае, f (x ₀) > f (x). Таким образом, мы доказали, что в точке x ₀ функция имеет локальный максимум.

Аналогично доказываются остальные утверждения теоремы.3

Пример 6.1. Исследовать на экстремум функцию .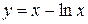

Найдем производную данной функции и определим критические точки первого рода.

.

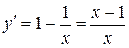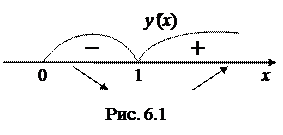Очевидно, что первая производная исходной функции обращается в ноль в точке x ₀ = 1 и не существует в точке x ₁ = 0. Однако из этих двух найденных точек, подозрительной на экстремум является только точка x ₀ = 1. Точка x ₁ = 0 не входит в область определения исходной функции и, следовательно, не является критической. Исследуем знак первой производной на всей области определения функции 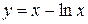, т.е. при всех x > 0 (рис. 6.1):

На промежутке x Î(0; 1) первая производная меньше нуля, следовательно функция убывает (обозначается y (x)¯). При
x Î(1; +¥) производная больше нуля, следовательно, функция возрастает (обозначается y (x)­). В точке x = 1 функция имеет минимум, причем y_min = y (1) = 1 – ln 1 = 1.

Задача 6.2. Исследовать на экстремум функцию .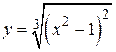

Решение. Найдем производную данной функции и определим критические точки первого рода.

.

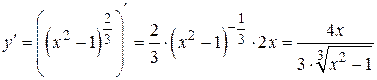Критическими точками первого рода данной функции являются точка
x ₁ = 0, в которой первая производная обращается в 0, и точки x ₂ = 1 и x ₃ = –1, в которых первая производная данной функции не существует. Заметим, что во всех найденных точках исходная функция определена и, следовательно, может иметь экстремум. Исследуем знак первой производной на всей области определения исходной функции 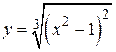, т.е. при всех действительных x (рис. 6.2):

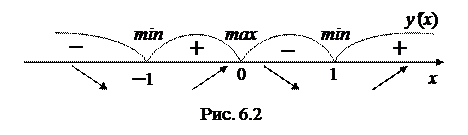В точках
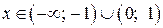первая производная меньше нуля, следовательно, функция убывает. В точках 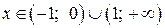производная больше нуля, следовательно, функция возрастает. В точках x = ±1 первая производная меняет знак с минуса на плюс, следовательно, функция в этих точках имеет минимум (y_min = y (±1) = 0). В точке x = 0 первая производная меняет знак с плюса на минус, следовательно, функция имеет максимум (y_max = y (0) = 1).

Заметим, что в приведенном примере функция имеет минимумы в тех точках, в которых первая производная не существует, т.е. не является гладкой. График исходной функции в этих точках имеет изломы (рис. 6.6).

§6.3. Направление выпуклости и точки перегиба
графика функции

Пусть функция y = f (x) дифференцируема на интервале (a; b). Тогда существует касательная к графику функции в любой точке A (x; f (x)) (x Î(a; b)), причем эта касательная не параллельна оси OY.

2 График дифференцируемой на интервале (a; b) функции y = f (x) называется выпуклым вверх (выпуклым), если он расположен не выше любой касательной, проведенной к графику на интервале (a; b) (рис. 6.3).

2 График дифференцируемой на интервале (a; b) функции y = f (x) называется выпуклым вниз (вогнутым), если он расположен не ниже любой касательной, проведенной к графику на интервале (a; b) (рис. 6.4).

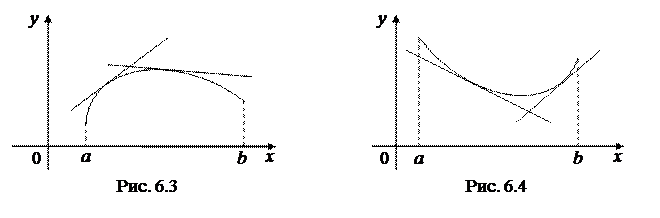2 Точки, отделяющие выпуклую часть графика функции от вогнутой (или наоборот), называются точками перегиба графика функции.

1 Если функция y = f (x) имеет на интервале (a; b) вторую производную, причем f² (x) > 0 (f² (x) < 0), то во всех точках интервала (a; b) график функции является вогнутым (выпуклым).

g Необходимое условие перегиба графика функции. Пусть график функции y = f (x) в точке М (x ₀; f (x ₀)) имеет перегиб, и пусть функция y = f (x) имеет в точке x ₀ непрерывную вторую производную. Тогда .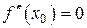

4Предположим противное, т.е. что 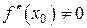. Тогда в силу непрерывности второй производной существует такая окрестность точки x ₀, в которой вторая производная имеет тот же знак, что и в точке x ₀. Следовательно, в этой окрестности график функции сохраняет направление выпуклости. Таким образом, в точке x ₀ график не имеет перегиба. 3

Замечание. Необходимое условие не является достаточным условием перегиба графика функции. В качестве простейшего примера можно привести функцию 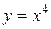. Вторая производная данной функции 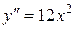обращается в ноль в точке x = 0, однако в этой точке график функции перегиба не имеет (очевидно, что в точке x = 0 функция 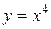имеет минимум).

2 Точки x ₀, в которых выполнено условие 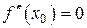, называются критическим точками второго рода.

Точки перегиба графика функции находятся из числа критических точек второго рода. Достаточным условием перегиба графика функции является следующая очевидная теорема.

1 Достаточное условие перегиба графика функции. Пусть существует такая d -окрестность 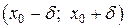точки x ₀, в которой функция y = f (x) имеет непрерывную вторую производную f² (x), принимающую значения разных знаков в интервалах 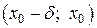и 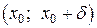(т.е. при переходе через точку x ₀ вторая производная меняет знак). Тогда в точке x ₀ график функции f (x) имеет перегиб.

1 Замечание. Достаточное условие перегиба остается верным в том случае, когда в самой точке x ₀ вторая производная не существует, но при этом в точке М (x ₀; f (x ₀)) существует касательная к графику функции y = f (x).

Пример 6.3. Определить участки выпуклости, вогнутости и точки перегиба графика функции .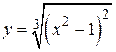

Первая производная данной функции 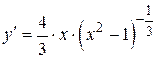была найдена ранее (пример 6.2). Найдем вторую производную данной функции и определим критические точки второго рода.

.

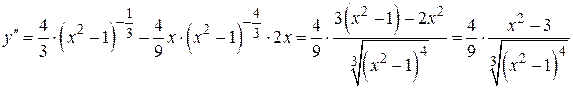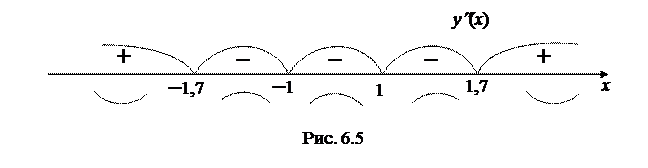Критическими точками второго рода данной функции являются точки 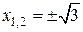, в которых вторая производная данной функции обращается в 0, и точки 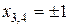, в которых вторая производная не существует. Исследуем знак второй производной (рис. 6.5) учитывая, что знаменатель дроби 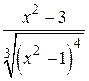положителен при всех .

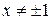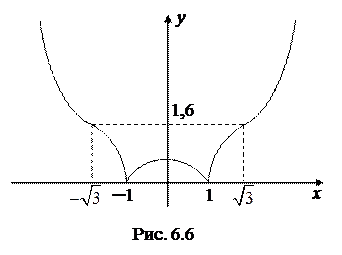На интервалах 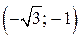, 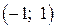и 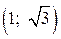вторая производная меньше нуля, следовательно, график функции является выпуклым. На интервалах 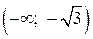и 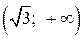вторая производная больше нуля, следовательно, график функции является вогнутым. В точках 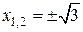вторая производная меняет знак, следовательно, график функции в этих точках имеет перегиб 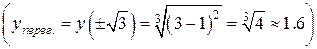. В точках 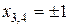вторая производная знака не меняет, следовательно, в этих точках перегиба нет (в примере 6.2 было установлено, что в точках 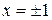функция имеет минимум). График функции, рассмотренной в примерах 6.2 и 6.3, изображен на рис. 6.6.