Экстремум функции. Монотонность

Предположим, что на некотором интервале (a, b) определена некоторая функция y = f (x).

2 Точка 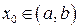называется точкой максимума (локального максимума) функции y = f (x), если существует такая окрестность (x ₀ – d; x ₀ + d) точки x ₀, для всех точек которой (" x Î(x ₀ – d; x ₀ + d)), отличных от точки x ₀, выполнено неравенство f (x) < f (x ₀). Аналогично определяются точки минимума.

2 Точка x ₀ называется точкой минимума (локального минимума) функции y = f (x), если существует такая окрестность (x ₀ – d; x ₀ + d) точки x ₀, для всех точек которой, отличных от точки x ₀, выполнено неравенство f (x) > f (x ₀). Точки максимума и минимума функции называются точками экстремума (локального экстремума).

1 Теорема Ферма. Пусть функция y = f (x) определена на некотором интервале (a, b) и в некоторой точке x ₀Î(a; b) имеет экстремум. Тогда, если в точке x ₀ существует производная, то она равна нулю (f¢ (x ₀) = 0).

1 Теорема Ролля. Пусть на отрезке [ a; b ] задана непрерывная функция
y = f (x), причем:

1) f (x) дифференцируема на интервале (a; b);

2) f (a) = f (b).

Тогда существует точка x ₀Î(a; b), в которой f¢ (x ₀) = 0.

1 Теорема Лагранжа. Пусть на отрезке [ a; b ] задана непрерывная функция y = f (x), дифференцируемая на интервале (a; b). Тогда существует точка с Î(a; b) такая, что справедлива формула

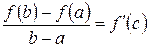. (6.1)
Равенство (6.1) можно переписать в виде формулы

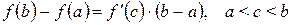. (6.2)

Формулу (6.2) называют формулой Лагранжа. Она связывает приращение функции на конечном отрезке с производной функции на этом отрезке.

Следствие. Если на некотором отрезке 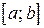производная функции тождественно равна нулю, то она является константой на данном отрезке.

2Функция называется возрастающей (неубывающей) на интервале (a; b), если она определена на данном интервале и для любых x ₁, x ₂Î(a; b) таких, что
x ₂ > x ₁, справедливо неравенство f (x ₂) > f (x ₁) (f (x ₂) ³ f (x ₁)).

2Функция называется убывающей (невозрастающей) на интервале (a; b), если она определена на данном интервале и для любых x ₁, x ₂Î(a; b) таких, что
x ₂ > x ₁, справедливо неравенство f (x ₂) < f (x ₁) (f (x ₂) £ f (x ₁)).

2Возрастающие и убывающие функции называют монотонными.

g Признак монотонности функции. Если функция f (x) дифференцируема на интервале (a; b) и f¢ (x) ³ 0 (f¢ (x) £ 0) на (a; b), то функция не убывает
(не возрастает) на (a; b).

4Предположим, что f¢ (x) ³ 0 для любого x Î(a; b), и пусть x ₁ и x ₂ две произвольные точки из (a; b) такие, что x ₂ > x ₁. Тогда на отрезке [ x ₁; x ₂] выполняются все условия теоремы Лагранжа. Согласно формуле (6.2) получим 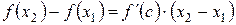, где с Î(x ₁; x ₂). По условию, оба сомножителя, стоящие в правой части полученного равенства, неотрицательны (f¢ (с) ³ 0,
x ₂ – x ₁ > 0). Тогда f (x ₂) – f (x ₁)³ 0 и, следовательно, f (x ₂) ³ f (x ₁). Случай f¢ (x) £ 0 доказывается аналогично. 3

Замечание 1. Если f¢ (x) > 0 (f¢ (x) < 0) на (a; b), то функция возрастает (убывает) на (a; b) (доказывается аналогично).

Замечание 2. Положительность (отрицательность) производной на интервале (a; b) не является необходимым условием возрастания (убывания) функции. Например, функция y = x ³ возрастает при всех x, однако в точке x = 0 имеет производную f¢ (0) = 0.