Рассмотрим класс квантовых систем, с независящим от времени гамильтонианом. Для таких систем решение уравнения (2.7) можно искать с помощью метода разделения переменных. Положим
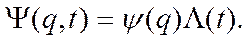
Подстановка такой функции 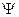 в уравнение (2.8), дает
в уравнение (2.8), дает
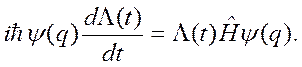
Разделяя переменные, имеем

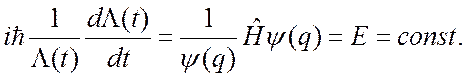
Отсюда временная составляющая 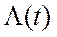 волновой функции, равна
волновой функции, равна
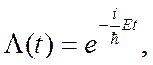 (2.9)
(2.9)
а волновая функция 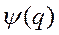 , зависящая только от пространственных переменных, удовлетворяет уравнению
, зависящая только от пространственных переменных, удовлетворяет уравнению
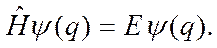 (2.10)
(2.10)
Из вида (2.10) следует, что это уравнение представляет собой уравнение для определения собственных значений 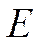 и собственных функций
и собственных функций 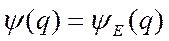 оператора энергии
оператора энергии 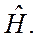 Таким образом, допустимое множество значений параметра
Таким образом, допустимое множество значений параметра 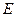 образует спектр энергии квантовой системы.
образует спектр энергии квантовой системы.
Частное решение уравнения Шредингера с независящим от времени гамильтонианом, имеет вид
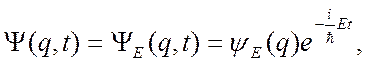 (2.11)
(2.11)
где 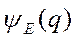 подчиняется уравнению (2.10). Уравнение (2.10) называется стационарным уравнением Шредингера, а состояния квантовой системы, описываемые волновыми функциями вида (2.11) – стационарными состояниями. Последнее название связано с тем, что плотность вероятности
подчиняется уравнению (2.10). Уравнение (2.10) называется стационарным уравнением Шредингера, а состояния квантовой системы, описываемые волновыми функциями вида (2.11) – стационарными состояниями. Последнее название связано с тем, что плотность вероятности
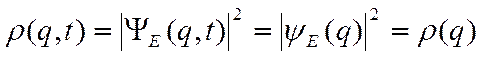
не зависит от времени 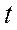 .
. 
Среднее значение физической величины 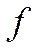 в стационарном состоянии с волновой функцией
в стационарном состоянии с волновой функцией 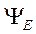 также не зависит от времени
также не зависит от времени
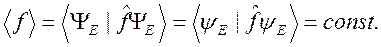
Общее решение рассматриваемой задачи будет представлять собой суперпозицию частных решение вида (2.11). Если спектр энергии имеет и дискретную и непрерывную составляющие, т.е.
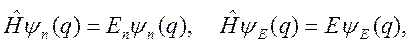
то общее решение уравнения Шредингера принимает вид
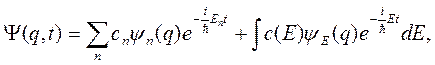 (2.12)
(2.12)
где 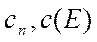 - коэффициенты. Для задачи Коши с начальным условием
- коэффициенты. Для задачи Коши с начальным условием 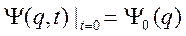 коэффициенты
коэффициенты 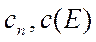 равны
равны
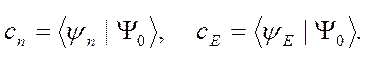 (2.13)
(2.13)
Следует отметить, что для задачи с вырождением в представлении (2.12) для волновой функции под квантовыми числами 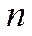 и
и 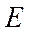 , по которым проводится суммирование и интегрирование, следует понимать наборы квантовых чисел, включая энергию, полностью определяющих квантовые состояния системы.
, по которым проводится суммирование и интегрирование, следует понимать наборы квантовых чисел, включая энергию, полностью определяющих квантовые состояния системы.
В качестве примера определим стационарные состояния для одномерного движения (вдоль оси 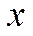 ) свободной квантовой частицы. Гамильтониан системы
) свободной квантовой частицы. Гамильтониан системы
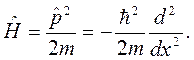 (2.14)
(2.14)
Стационарное уравнение Шредингера имеет вид
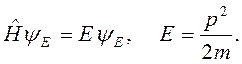 (2.15)
(2.15)
 Так как гамильтониан коммутирует с оператором импульса, то операторы
Так как гамильтониан коммутирует с оператором импульса, то операторы 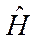 и
и 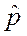 имеют общую систему собственных функций. Нетрудно проверить, что собственные функции оператора импульса
имеют общую систему собственных функций. Нетрудно проверить, что собственные функции оператора импульса
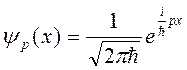 (2.16)
(2.16)
удовлетворяют уравнению (2.15), т.е. является собственной функций оператора 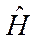 . Таким образом, в соответствие с (2.11), волновые функции стационарных состояний для свободной частицы имеют вид
. Таким образом, в соответствие с (2.11), волновые функции стационарных состояний для свободной частицы имеют вид
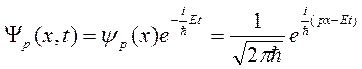 ,
,
т.е. представляют собой волны де Бройля (см. (2.2)).. Общее решение уравнения Шредингера (2.7) есть суперпозиция волн де Бройля:
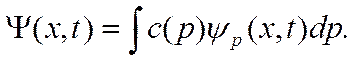
(2.17)
Следовательно, волновая функция свободной частицы есть волновой пакет.
 2015-04-17
2015-04-17 385
385








