Уравнение непрерывности. Рассмотрим квантовую частицу с массой , находящуюся в потенциальном поле

Рассмотрим квантовую частицу с массой 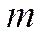, находящуюся в потенциальном поле 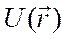. Гамильтониан системы имеет вид (2.6). Выпишем уравнение Шредингера для рассматриваемой системы:

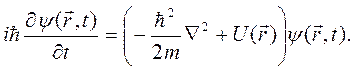
(2.18)

Относительно волновой функции 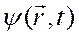предполагается, что она непрерывна вместе со своими частными производными по координатам, включая поверхности разрыва потенциала 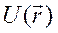. Предполагается также, что задано начальное условие 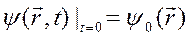и волновая функция квадратично интегрируема

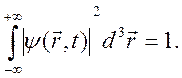(2.19)

При этих условиях решение уравнение Шредингера (2.18) существует и определяется однозначно. Покажем, что сделанных предположениях, все решения уравнения Шредингера (2.18) подчиняются, так называемому, уравнению непрерывности.

Применим к обеим частям уравнения (2.18) операцию комплексного сопряжения, получим

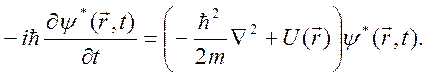
(2.20)

Далее уравнения (2.18) и (2.20) умножим соответственно на функци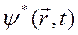и и 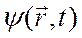и из первого результата вычтем второй, получим

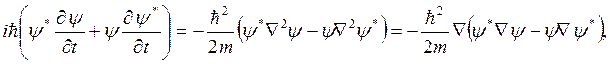
или

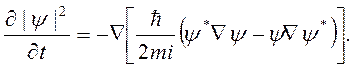
Выражение под знаком производной слева есть плотность вероятности 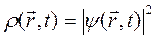. Обозначим выражение в скобках, на которое действует оператор 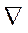через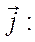

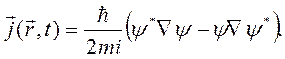(2.21)

Таким образом, искомое уравнение принимает вид

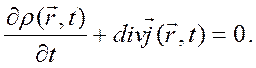(2.22)

Поскольку производная по времени от 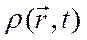характеризует скорость изменения плотности вероятности обнаружить частицу в окрестности точки 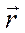, то полученное уравнение (2.22) имеет по аналогии с механикой сплошной среды и классической электродинамикой вид уравнения непрерывности, если вектор 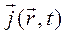интерпретировать как вектор плотности тока вероятности.

Динамика средних физических величин

Рассмотрим физическую величину 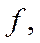оператор которой 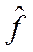, зависит от времени. Рассмотрим среднее этой величины в некотором состоянии :

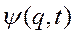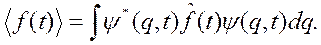
Определим скорость изменения среднего 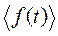со временем

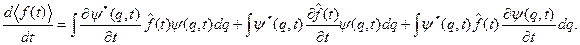
Из уравнения Шредингера имеем

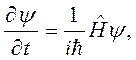
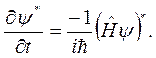
После подстановки производных, с учетом, что 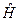эрмитов оператор, получаем

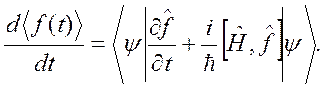(2.23)

В соответствие с общим определением среднего физической величины в заданном квантовом состоянии, оператор

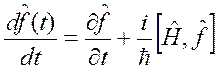(2.24)

будем интерпретировать как оператор скорости изменения физической величины 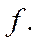Таким образом

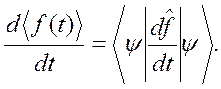(2.25)

Теоремы Эренфеста.

Рассмотрим одномерное движение квантовой частицы в потенциале 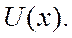Гамильтониан системы 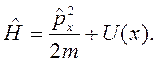Используя уравнение (2.24) определим изменение во времени операторов координаты и импульса. Для оператора координаты имеем

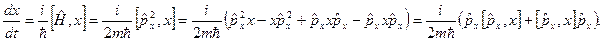
Используя выражение для коммутатора 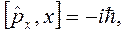для оператора скорости, получаем

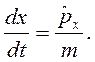(2.26)

Аналогично для оператора импульса

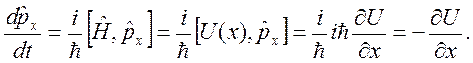
Окончательно

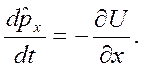(2.27)

Для средних значений из (2.26), (2.27), получаем систему уравнений

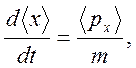
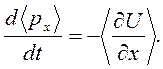(2.28)

Полученные уравнения представляют собой квантовый аналог канонических уравнений Гамильтона. Объединяя оба эти уравнения, приходим к обобщению на квантовый случай уравнения Ньютона

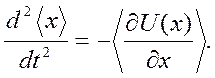(2.29)

Результаты (2.28),(2.29) составляют содержание, так называемых, теорем Эренфеста.

Подчеркнем, что уравнение (2.29) для произвольного потенциала не является замкнутым.

Это легко видеть, если разложить функцию 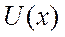в степенной ряд Тейлора. При этом среднее 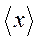зависит от бесконечной совокупности моментов более высокого порядка.

Рассмотрим переход к классическому уравнению движения. Предположим, что состояние 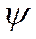представляет собой волновой пакет, локализованный в окрестности точки 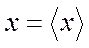. Разложим функцию 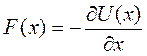в ряд по степеням отклонения 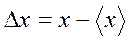, ограничиваясь квадратичными членами:

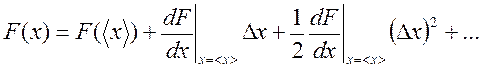
После усреднения обеих частей, получаем

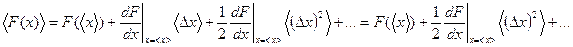
Здесь учтено, что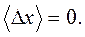

Таким образом, уравнение движения (2.29), принимает вид

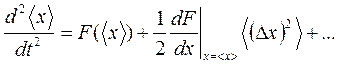
При условии

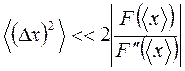(2.30)

движение центра волнового пакета описывается классическим уравнением Ньютона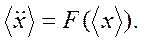

Более строго, по-мимо условия (2.30), нужно учесть еще квантовую специфику задачи – соотношение неопределенностей для координаты и импульса 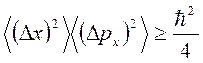. Потребуем малость флуктуаций импульса относительно среднего значения 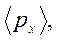имеем 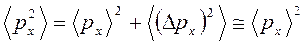при

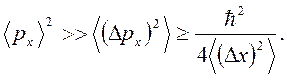
Таким образом, классическое уравнение движения получается для квантовой частицы, движущейся с относительно большим импульсом в плавно меняющемся внешнем поле. При этом функция Гамильтона имеет вид

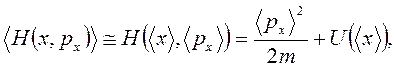
т.е. можно говорить о движении центра пакета по траектории.

Законы сохранения.

Представление (2.24), (2.25) удобно для установления интегралов движения, т.е. физических величин средние от которых не меняются во времени. Из определения (2.24) видно, что если оператор 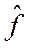не зависит явно от времени и коммутирует с гамильтонианом, то

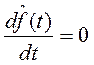
и из выражения (2.25), получаем, что

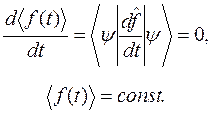(2.31)

При сформулированных таким образом условиях, величина 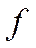сохраняется, т.е. является интегралом движения.

На практике, значительная часть операторов физических величин, не зависит явно от времени. К их числу относятся операторы координаты, импульса, момента импульса, энергии (с гамильтонианами вида (2.6) (2.7)) и т.п.

Для таких операторов соответствующие им физические величины сохраняются, если они коммутируют с гамильтонианом:

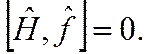(2.32)