На практике операционные методы получили широкое применение для отыскания решений линейных дифференциальных уравнений и линейных систем дифференциальных уравнений с постоянными коэффициентами.
Решение задачи Коши для линейного дифференциального уравнения n - го порядка с постоянными коэффициентами
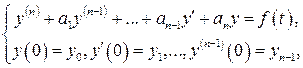
(здесь y 0, y 1, …, yn -1 - заданные постоянные) может быть получено операционным методом по следующей формуле:
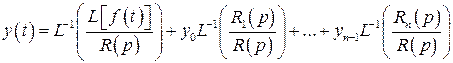 , (2)
, (2)
где
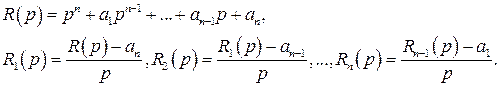
Решение задачи Коши для линейной системы дифференциальных уравнений n - го порядка с постоянными коэффициентами

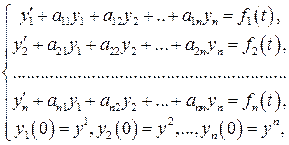
(здесь y 1, y 2,…, yn - заданные постоянные) может быть получено операционным методом по следующей формуле:
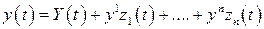 , (3)
, (3)
где
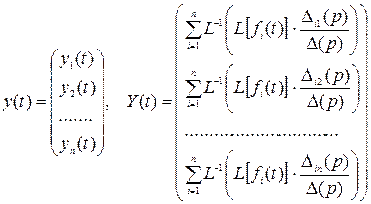 ,
,
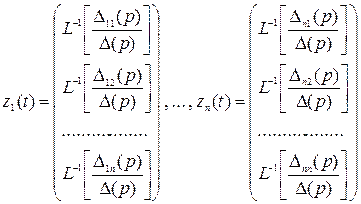 ,
,
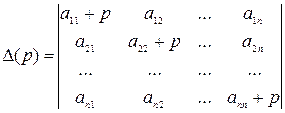 ,
, 
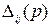 - алгебраические дополнения элементов определителя
- алгебраические дополнения элементов определителя 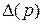 .
.
Задание 1. Найти решение задачи Коши для дифференциального уравнения 2-го порядка:
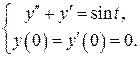
Решение. В данном случае 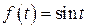 . Следовательно, по второй формуле малой таблицы лапласовых изображений имеем:
. Следовательно, по второй формуле малой таблицы лапласовых изображений имеем: 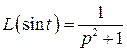 . Тогда в силу (2) решение задачи Коши для данного дифференциального уравнения может быть записано в виде:
. Тогда в силу (2) решение задачи Коши для данного дифференциального уравнения может быть записано в виде:
|
|
|
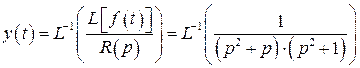 .
.
Для нахождения обратного преобразования Лапласа полученной правильной дробно-рациональной функции, найдем ее разложение на простейшие:
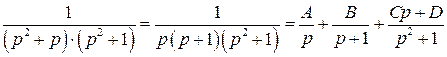 ,
,
где коэффициенты A, B,C,D находятся как решение системы алгебраических уравнений:
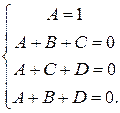
Решая систему, получаем: 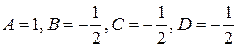 . Следовательно,
. Следовательно, 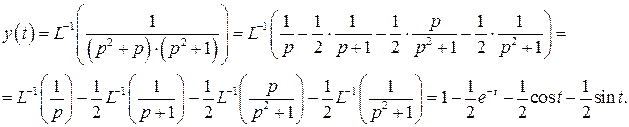
(Здесь мы воспользовались свойством линейности обратного преобразования Лапласа и малой таблицей обратных преобразований Лапласа.)
Задание 2. Найти решение задачи Коши для системы дифференциальных уравнений:
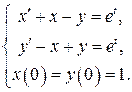
Решение. В данном случае 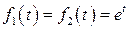 . Следовательно, по первой формуле малой таблицы лапласовых изображений имеем:
. Следовательно, по первой формуле малой таблицы лапласовых изображений имеем: 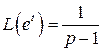 . Тогда в силу (3) решение задачи Коши для данной системы дифференциальных уравнений может быть представлено в виде:
. Тогда в силу (3) решение задачи Коши для данной системы дифференциальных уравнений может быть представлено в виде:
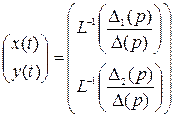 ,
,
где
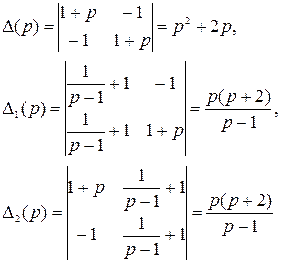
Следовательно,
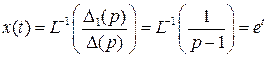 ,
,
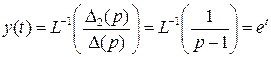 .
.
 2015-04-01
2015-04-01 514
514








