Импликантная матрица представлена табл.4.9. Ядром нашей функции являются импликанты 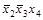 ,
, 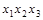 ,
, 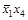 . Импликант
. Импликант 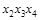 – лишний, т.к. ядро накрывает все столбцы импликантной матрицы. Поэтому, функция имеет единственную тупиковую и минимальную ДНФ
– лишний, т.к. ядро накрывает все столбцы импликантной матрицы. Поэтому, функция имеет единственную тупиковую и минимальную ДНФ 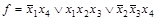 .
.
Таблица 4.9
| Простые импли-канты | Номера конституент единицы | ||||||
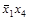
| * | * | * | * | |||
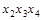
| * | * | |||||
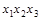
| * | * | |||||
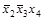
| * | * |
Пример 4.2. Минимизировать булеву функцию 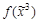 методом Квайна:
методом Квайна:
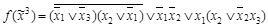
1. Получим функцию в СДНФ
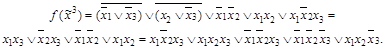
2. Найдем сокращенную ДНФ функции f, произведя все возможные склеивания и поглощения:
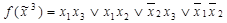
3. Получим МДНФ функции 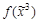 по импликантной матрице (табл. 4.10). Ядро булевой функции:
по импликантной матрице (табл. 4.10). Ядро булевой функции: 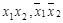 . Функция имеет две тупиковые ДНФ. Они же являются минимальными ДНФ
. Функция имеет две тупиковые ДНФ. Они же являются минимальными ДНФ
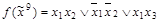
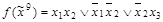
Таблица 4.10
| Простые импли-канты | Конституенты | ||||
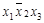
| 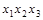
| 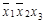
| 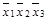
| 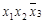
| |
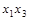
| * | * | |||
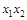
| * | * | |||
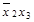
| * | * | |||
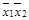
| * | * |
При программной реализации метода Квайна конъюнкции, подлежащие склеиванию, разбивают на группы. В i -ю группу включают конъюнкции, содержащие i переменных без отрицания. Тогда на склеивание нужно проверять только конъюнкции соседних групп, при этом перебор сокращается. Сами конъюнкции удобно кодировать двумя двоичными векторами 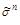 (вектор вхождения) и
(вектор вхождения) и 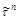 (вектор обращения), элементы которых определяются следующим образом:
(вектор обращения), элементы которых определяются следующим образом:
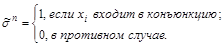
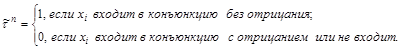
Например, конъюнкция 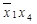 может быть сохранена с помощью векторов
может быть сохранена с помощью векторов 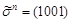 и
и  . Данные вектора удобно хранить в битовой форме.
. Данные вектора удобно хранить в битовой форме.
При большом числе аргументов наиболее трудоемким является этап, связанный с отысканием наилучшего покрытия импликантной матрицы (сокращенная ДНФ и сама матрица находятся сравнительно быстро). Поэтому, для осуществления этого этапа обычно используют приближенные методы, не гарантирующие нахождения МДНФ. Один из таких методов состоит в следующем:
1. Ищется ядро логической функции. Столбцы, покрытые ядром, вычеркиваются из таблицы.
2. Дальнейший выбор импликантов осуществляется с использованием следующей пошаговой процедуры. В новой таблице берется строка с наибольшим числом символов * (если таких строк несколько, то любая из них). Эта строка и столбцы, в которых она содержит * из таблицы вычеркиваются, а соответствующий ей импликант включается в покрытие. К полученной таблице применяется та же операция и т.д., пока все столбцы не окажутся вычеркнутыми.
Если требуется нахождение всех тупиковых ДНФ (всех покрытий импликантной матрицы), то можно воспользоваться следующим методом (метод Петрика). По импликантной матрице строится так называемое конъюнктивное представление матрицы. Для этого все строки (простые импликанты) обозначаются разными буквами. После этого, для каждого i -го столбца матрицы строится дизъюнкция всех букв, обозначающих строки матрицы, пересечение которых с i -м столбцом отмечено *. Конъюнктивное представление матрицы образуется как конъюнкция построенных дизъюнкций для всех столбцов матрицы. К конъюнктивному представлению матрицы могут быть применены все соотношения булевой алгебры с целью его упрощения. После раскрытия скобок и выполнения всех возможных поглощений получается дизъюнкция конъюнкций, каждая из которых соответствует покрытию матрицы, т.е, тупиковой ДНФ функции.
Пример 4.3. Импликантная матрица функции 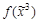 задана табл.4.10. Найти методом Петрика все тупиковые ДНФ функции
задана табл.4.10. Найти методом Петрика все тупиковые ДНФ функции 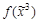 . Имеющиеся простые импликанты обозначим буквами:
. Имеющиеся простые импликанты обозначим буквами:
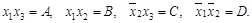
Тогда конъюнктивное представление матрицы имеет вид
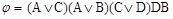
После упрощения получим 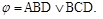 Т.о., функция имеет две тупиковые ДНФ:
Т.о., функция имеет две тупиковые ДНФ:
 2015-04-01
2015-04-01 556
556







