2015-04-30
1495
В общем случае под градиентными методами понимают методы, в которых направление движения к точке оптимума функции совпадает с направлением градиента этой функции. Градиентные методы относятся к приближенным методам решения задач нелинейного программирования. В общем случае они обеспечивают получение оптимального решения с помощью бесконечного процесса последовательных приближений. Однако, в некоторых случаях процесс может закончиться и через конечное число итераций.
Градиентные методы могут применяться к любой задаче нелинейного программирования, приводя лишь к локальному, а не глобальному экстремуму. Поэтому они оказываются более эффективными при решении задач выпуклого программирования, где всякий локальный экстремум есть одновременно и глобальный.
Общая постановка задачи соответствует (5.1) и (5.2). Однако, не теряя общности, она может быть преобразована к виду
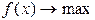(5.53)
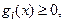
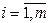(5.54)
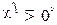
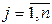(5.55)
Математическая стратегия градиентного метода заключается в следующем. Выбирается произвольная допустимая точка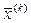 
. Для перехода в результате итераций от точки 
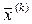к точке 
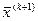в 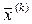определяют такое направление 
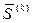, чтобы при достаточно малом 
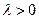луч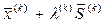 
принадлежал допустимой области. То есть следующая точка итерационного процесса определяется по формуле:
|
|
|
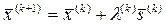(5.56)
Различие градиентных методов состоит в способе определения направления 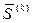и параметра 
.
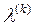Выбор направления :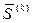
1. Если 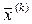- внутренняя точка области допустимых решений, то
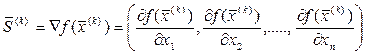(5.57)
есть градиент функции в точке 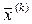. Стратегия, выражаемая соотношением (5.57) определяет движение с переменным шагом, так как значение шага зависит от значения градиента 
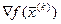. Поскольку значение градиента уменьшается вблизи оптимума, то на некоторых участках шаги будут мелкими, что удлиняет время поиска. От этого недостатка можно избавиться, если использовать градиентную стратегию с постоянным шагом. В этом случае вектор градиента 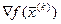заменяется на вектор направления градиента:
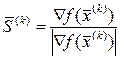(5.58)
где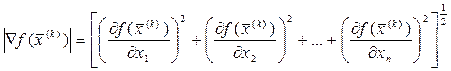 
2. 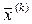не принадлежит допустимой области. Это может иметь место в случае, если точка, двигаясь в сторону наибольшего возрастания функции нарушила i -ое ограничение (5.54). В качестве штрафа за нарушение i -ого ограничения введем множитель Ri и вспомогателную целевую функцию.
L(x) = f(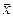
) 
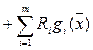
Если под целевой функцией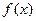 
понимать доход предприятия, то 
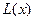есть ни что иное, как доход предприятия за вычетом штрафных санкций.
В простейшем случае Ri выбирается следующим образом:
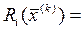
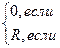
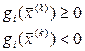(5.59)
Число R должно быть достаточно большим, чтобы заставить двигаться точку внутрь допустимой области. Направление движения точки в этом случае задается вектором
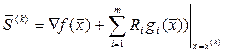(5.60)
Недостаток этой стратегии в том, что точность вычислений напрямую зависит от выбора числа R. При неудачном выборе числа R итерационный процесс будет характеризоваться резкими колебаниями точки возле границы.
|
|
|
Данного недостатка можно избежать, если принять что штраф должен быть тем меньше, чем меньшее нарушение может иметь место, то есть целесообразно предположить, что
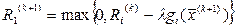(5.61)
Выбор параметра :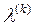
1) Параметр 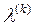число постоянное на всех итерациях. Чем меньше число 
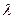, тем точнее вычисления. Соответственно увеличивается и время поиска оптимума;
2) Параметр 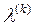выбирают на каждом шаге из условия min{ λ′‚ λ″ }, где λ’ – значение параметра, при котором луч 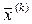+ λ ( k ) S ( k ) пересекает ОДЗ; λ″ - такое допустимое значение λ, при котором функция f( 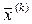+ λ ( k ) S ( k ) ) достигает максимума на луче. Данная стратегия позволяет находиться в точке ОДЗ и оптимизировать количество итераций. Однако, при нелинейных ограничениях и нелинейной целевой функции вычисление λ’, λ″ может оказаться достаточно трудоемким.
Для иллюстрации градиентного метода выберем следующую стратегию: λ – число постоянное; величина штрафа пропорциональна величине нарушения ограничения; направление движения точки совпадает с направлением градиента. Это так называемый градиентный метод Эрроу-Гурвица. Если ограничения по знаку (5.55) отсутствуют, то координаты новой точки можно рассчитать в соответствии с (5.56), (5.60) по формуле:
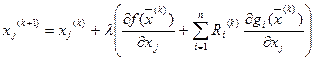(5.62)
С учетом условия неотрицательности (5.55), выражение (5.62) будет выглядеть:
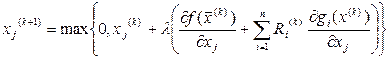(5.63)
В выражениях (5.62) и (5.63) функция штрафа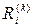 
вычисляется по формуле (5.61).
Пример 5.3 Требуется максимизировать функцию
F (x)= - x 12- x 22 при условии -(x 1-2)2 – (x 2-2)2 + 1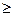 
0
Пусть λ =0.1; R 1(0)=2; x 1(0)=3; x 2(0)=1.5, то есть мы выбрали начальную точку, заведомо не принадлежащую допустимой области.
Уравнения (5.62) имеют следующий вид:
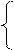
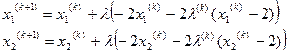
Уравнения (5.61) имеют следующий вид:
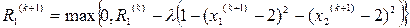
Первая итерация:
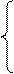
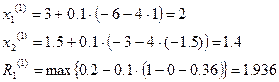
Вторая итерация: Точка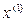 
находится уже внутри допустимой области, однако, множитель 
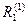, хотя и меньше 
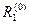, но еще отличен от 0 и граница продолжает «подталкивать» движущуюся точку внутрь допустимой области (эта точка еще находится на «опасном расстоянии» от границы):
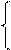
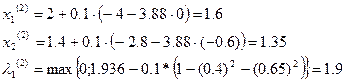
Подобным образом этот процесс можно продолжить и дальше. При увеличении числа итераций точка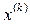 
при выполнении условия выпуклости целевой функции стремится к решению поставленной задачи.
Список рекомендованной литературы
1. А. В. Кузнецов, И. И. Холод. Математическое программирование. - Минск: «Высшая школа»,!984. – 221 с.
2. Вітлінський В.В., Наконечний С.І., Терещенко Т.О. Математичне програмування: Навч.-метод. Посібник для самост. Вивч. Диск. – к.: КНЕУ, 2001. – 248с.
3. Г.Г. Цегелик. Лiнiйне програмування.- Л.: «Свiт», 1995. – 216 с.
4. Зайченко Ю.П. Исследование операций: Учеб. пособие для студентов вузов. – 2-е изд., перераб. и доп. – Киев: Вища школа. Главное изд-во, 1979. 392 с.
5. И. А. Акулич. Математическое программирование в примерах и задачах. - М.: «Высшая школа», 1986.- 319 с.
6. Индивидуальные задания для выполнения контрольных работ по курсу «Математическое программирование» (Линейное программирование) для студентов экономических специальностей всех форм обучения.// Сост.: Глущевский В.В., ст. преподаватель, Исаенко А.Н., ст. преподаватель, - Запорожье: ЗГИА, 2002г. – 66с.
7. Лекции по теории графов /Под ред. Емеличева В.А. и др. - М.: Наука, 1990.
8. Майника Э. Алгоритмы оптимизации на сетях и графах. - М.: Мир, 1981.
9. С. Гасс. Линейное программирование. - М.: «Наука», 1961.-303 с.
10. Сакович В.А. Исследование операций (детерминированные методы и модели): Справочное пособие. - Мн.: Выш. шк., 1984.-256с.
11. Таха Х. Введение в исследование операций: в двух книгах. Кн.1,2 Пер. с англ. - М.: Мир, 1985.
12. Хазанова Л.Э. Математическое программирование в экономике: Учебное пособие. – М.: Издательство БЕК, 1998. – 141с.
|
|
|
