1. 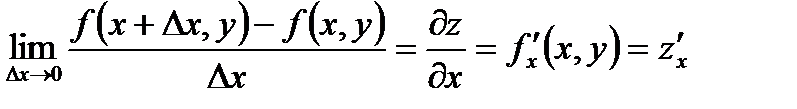 - частная производная 1-го порядка функции z по переменной x.
- частная производная 1-го порядка функции z по переменной x.
2. 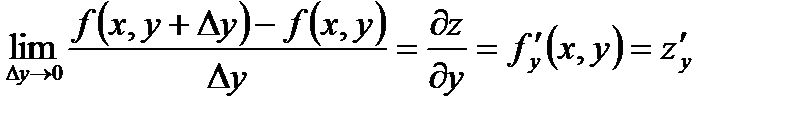 - частная производная 1-го порядка функции Z по переменной y.
- частная производная 1-го порядка функции Z по переменной y.
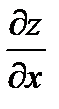 вычисляется при постоянном y,
вычисляется при постоянном y, 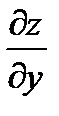 вычисляется при постоянном x.
вычисляется при постоянном x.
При вычислении 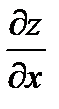 ,
, 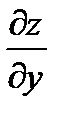 используются правила и формулы дифференцирования (смотреть таблицу производных).
используются правила и формулы дифференцирования (смотреть таблицу производных).
полный дифференциал функции
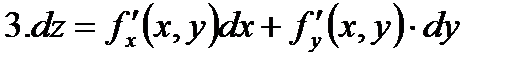
|
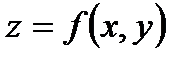
|
где 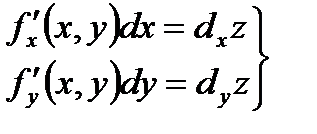 - частные дифференциалы
- частные дифференциалы
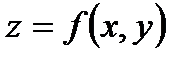
|
4.
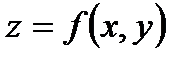
|
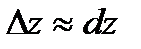
|
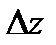
|
а), где - полное приращение функции.
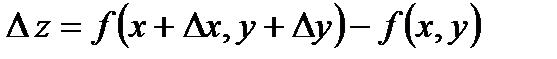
|
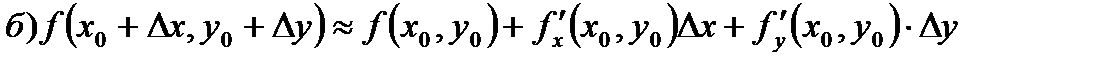
|
Эта функция используется в нахождении приближённых значений функции.
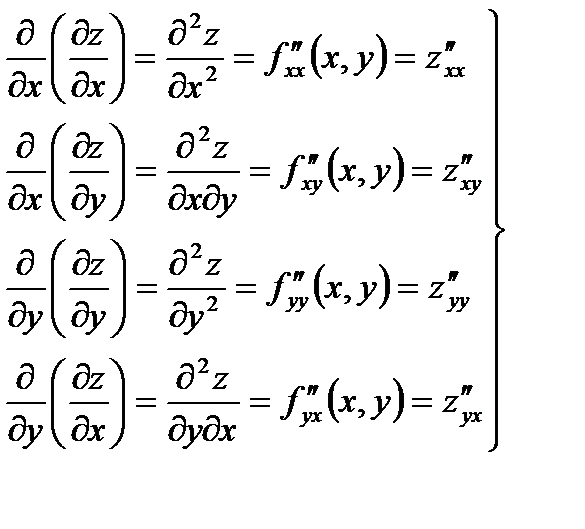
|
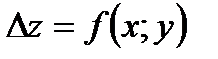 называются частные производные от её частных производных первого
называются частные производные от её частных производных первого
- Обозначения частных производных 2-го порядка от функции z= f(x,y), причём 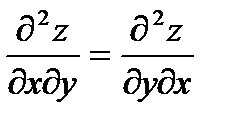
|
6. 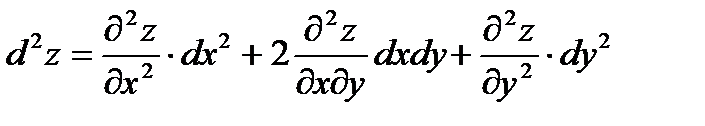 - дифференциал второго порядка для функции
- дифференциал второго порядка для функции 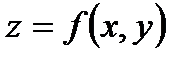
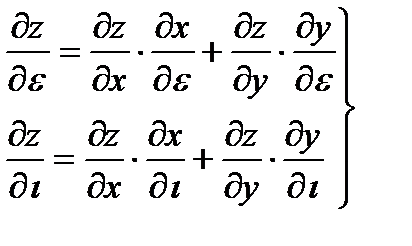
|
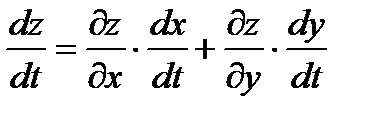 - производная сложной функции. z=f(φ(t),ψ(t)).
- производная сложной функции. z=f(φ(t),ψ(t)).
8. Если z=f(x,y), где 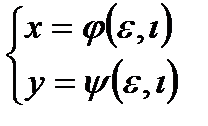 то
то
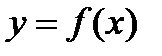
|
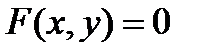
|
вычисляется по формуле:
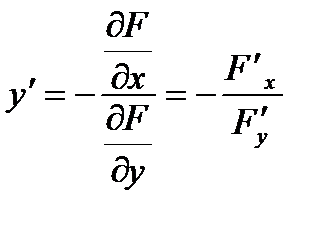
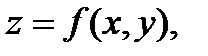
|
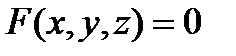
|
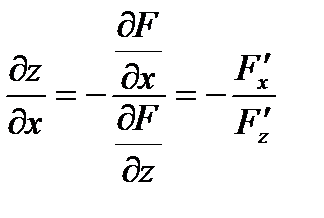
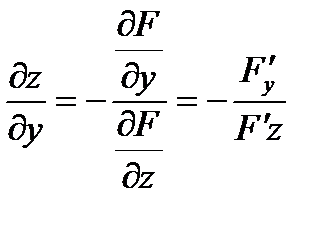 при условии
при условии 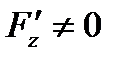
9.3 Примеры решения задач.
Задача 1.
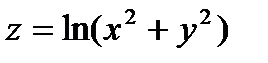
|
| функции |
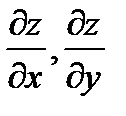 .
.
Решение:
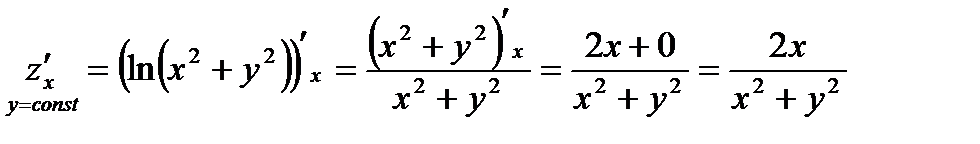
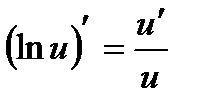 , где
, где 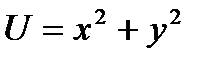
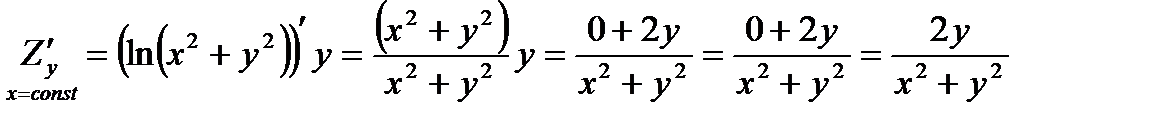
Задача 2. Найти полный дифференциал функции z= x3y+ xtgx
Решение:
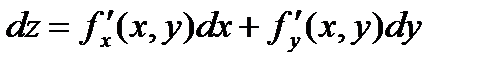
|
- теоретическая формула.
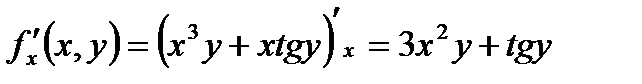
|
Где
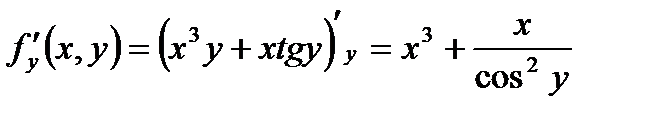
| -ответ |
| Тогда |
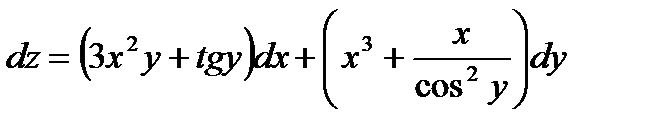
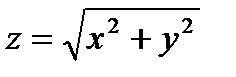
|
Задача 3. Вычислить приближённое значение функции в точке P(2,97;4,02)
Решение:
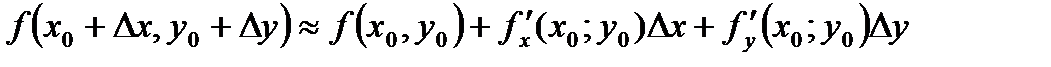
т.Р 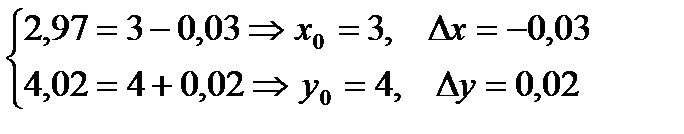
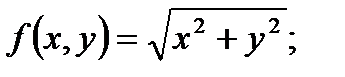
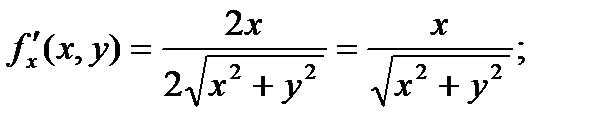
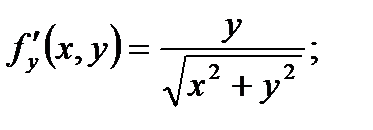
Тогда 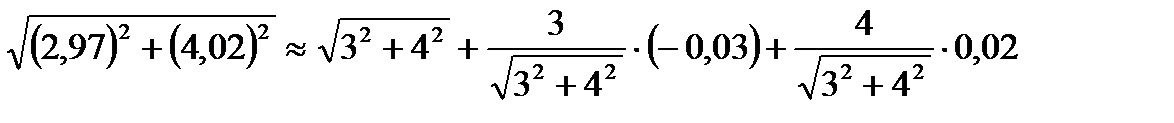
Или 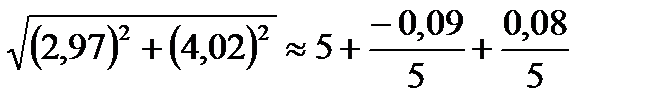
Или 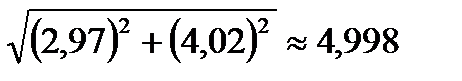
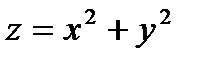
|
Задача 4. Найти производную функции в направлении, составляющим с положительным направлением оси (ОХ) угол a=60°.
Решение:
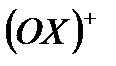
|
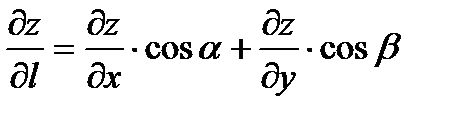 , где aи b- углы наклона вектора
, где aи b- углы наклона вектора 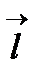 к оси и к оси (OY)+ соответственно.
к оси и к оси (OY)+ соответственно.
a=60°, тогда b=30° 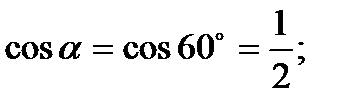
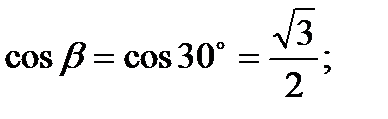
| тогда |
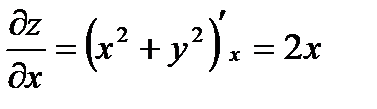
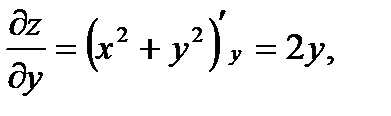
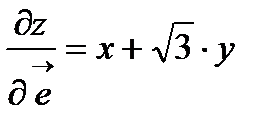 - ответ.
- ответ.
Задача 5. Вычислить градиент функции 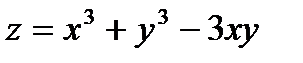 в точке А (2;1).
в точке А (2;1).
Решение:
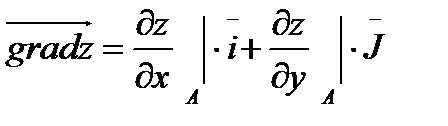 , где
, где 
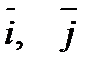 - базисные векторы, орты.
- базисные векторы, орты.
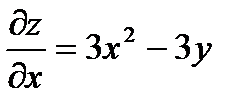
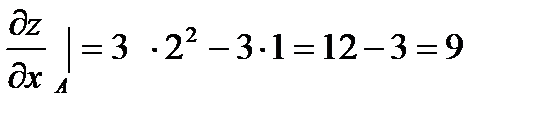
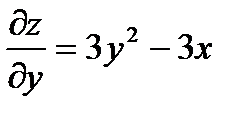
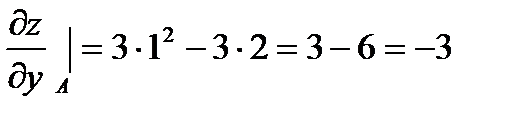
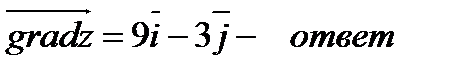
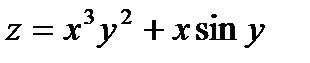
|
Задача 6. Найти смешанные частные производные второго порядка функции
Решение:
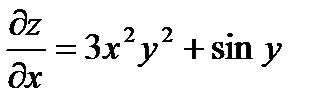
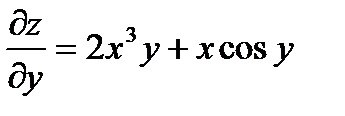
Дифференцируя, 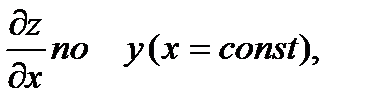 получаем
получаем 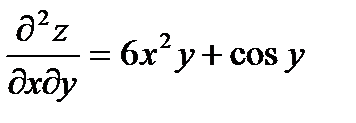
Дифференцируя 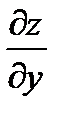 по x(y=const), получаем
по x(y=const), получаем 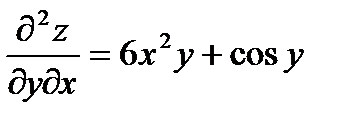
Ответ: 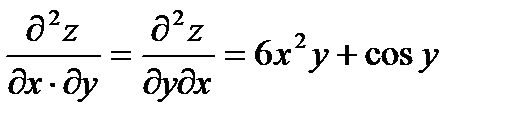
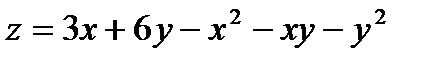
|
Задача 7. Исследовать на экстремум функцию
Решение: (1) 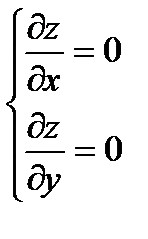 - необходимое условие экстремума.
- необходимое условие экстремума.
(2) 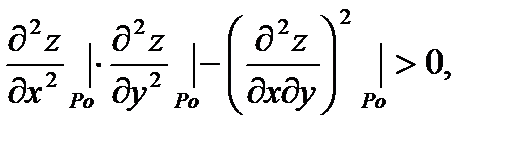 где
где 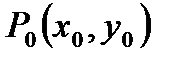 является решением системы (1).
является решением системы (1).
Неравенство (2) является достаточным условием экстремума.
Причём, если 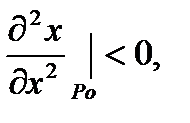 то в точке
то в точке 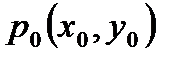 есть максимум функции.
есть максимум функции.
И если 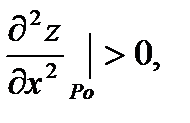 то в точке
то в точке 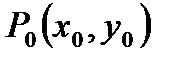 есть минимум функции.
есть минимум функции.
Имеем: 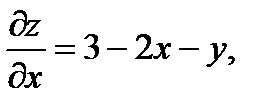
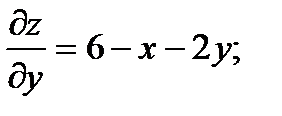
(1) 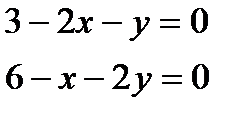 Þ
Þ 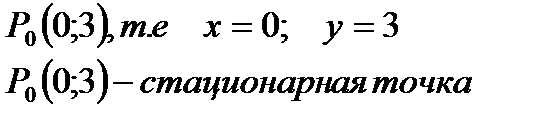
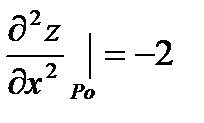
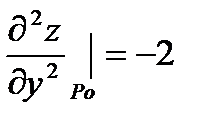
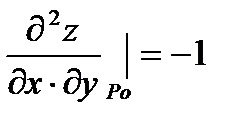
| есть экстремум, причём т.к |
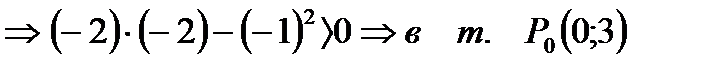
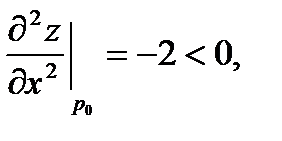
то в точке P0(0;3) есть максимум
Ответ: 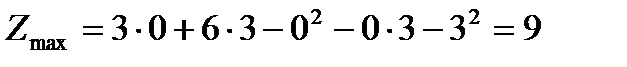
 2015-04-20
2015-04-20 582
582








