Интегральное исчисление
Разложение рациональной функции на простейшие дроби и их интегрирование
Предварительные сведения из алгебры
а) Если a вещественный корень многочлена, то существует единственное представление многочлена в виде
P(x) = (x – a)a P1(x), a³1, P1(a)¹0.
Число a называется кратностью корня. Другое эквивалентное определение кратности корня дается через производную. a – это порядок первой, не равной нулю производной в точке a: P(a)= P¢(a)=…= P(a-1)(a)=0, P(a)(a)¹0.
б) Если w = u + i v, v¹0 комплексный корень многочлена с действительными коэффициентами, то сопряженное комплексное число 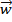 = u - i v также является корнем многочлена. Тогда существует единственное представление многочлена в виде
= u - i v также является корнем многочлена. Тогда существует единственное представление многочлена в виде
P(x) = (x2+px+q)b P1(x), b³1, P1(w)¹0,
(x - w)(x - 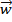 )=(x - u - i v)(x - u + i v)= x2+px+q.
)=(x - u - i v)(x - u + i v)= x2+px+q.
в) Любой многочлен можно разложить в произведение по своим корням
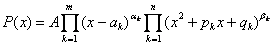 ,
,
где a1,a2,…-действительные корни кратностей a1,a2,… в количестве m штук, а w1,w2,… комплексные корни кратностей b1,b2,…. Связь между корнями и сомножителями в разложении многочлена следующая x2+pkx+qk=(x - wk)(x - 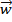 k).
k).
|
|
|
Определение. Рациональная функция (отношение двух многочленов) 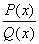 называется правильной дробью, если порядок многочлена числителя строго меньше порядка многочлена в знаменателе.
называется правильной дробью, если порядок многочлена числителя строго меньше порядка многочлена в знаменателе.
Утверждение. Любую рациональную функцию можно представить в виде многочлена (целая часть) плюс правильная дробь.
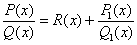 , - R(x) – многочлен, дробь
, - R(x) – многочлен, дробь 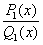 - правильная.
- правильная.
Условный экстремум Достаточные условия.
Пусть в точке x0= 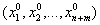 выполнены необходимые условия экстремума. Вопрос о наличии экстремума в этой точке зависит от поведения Df=f(x) – f(x0) при условии, что xÎD1 (область определяемая уравнениями связи). Для таких точек DFI = 0, поэтому Df = DL, и вопрос исследования поведения Df сводится к исследованию поведения приращения функции Лагранжа DL. По формуле Тейлора Правило Лопиталя Примеры решения и оформления задач контрольной работы
выполнены необходимые условия экстремума. Вопрос о наличии экстремума в этой точке зависит от поведения Df=f(x) – f(x0) при условии, что xÎD1 (область определяемая уравнениями связи). Для таких точек DFI = 0, поэтому Df = DL, и вопрос исследования поведения Df сводится к исследованию поведения приращения функции Лагранжа DL. По формуле Тейлора Правило Лопиталя Примеры решения и оформления задач контрольной работы
DL = 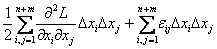 , eij®0 при Dxi®0. Теорема Лагранжа
, eij®0 при Dxi®0. Теорема Лагранжа
Если выразить «зависимые» Dxi через Dxi независимых переменных (это можно сделать продифференцировав уравнения связи), то можно получить выражение для DL следующего вида
DL =  , hij®0 при Dxi®0.
, hij®0 при Dxi®0.
После этого можно использовать условия для «безусловных» экстремумом для квадратичной формы 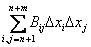 .
.
 2015-05-05
2015-05-05 518
518








