Впервые эти теоремы нашел александрийский математик Папп в 3 веке н.э.
В эпоху средневековья многие достижения античной науки были в Европе утрачены. В 17-ом веке теоремы вновь открыл швейцарский математик Гульдин.
Первая теорема Паппа-Гульдина. Площадь поверхности, образованной вращением кривой вокруг не пересекающей её оси, равна произведению длины кривой на путь, проходимый центром тяжести этой кривой.
В случае вращения вокруг оси  теорема записывается формулой
теорема записывается формулой
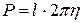 .
.
Доказательство. Рассмотрим случай плоской кривой, когда она задана явно уравнением 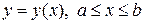 . Ордината центра тяжести кривой находится по формуле
. Ордината центра тяжести кривой находится по формуле 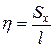 . Подставив сюда формулу для нахождения статического момента и умножив это равенство на длину кривой
. Подставив сюда формулу для нахождения статического момента и умножив это равенство на длину кривой 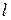 , получаем
, получаем
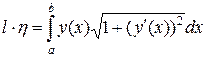 .
.
Затем домножим обе части этого равенства на 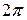 :
:
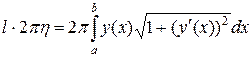 .
.
В правой части этого равенства стоит площадь поверхности тела, образованного вращением кривой вокруг оси  .
.
В левой части равенства стоит произведение длины кривой 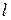 на длину окружности
на длину окружности 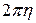 , которую описывает центр тяжести. Теорема доказана.
, которую описывает центр тяжести. Теорема доказана.
|
|
|
Пример 1. Найти координаты центра тяжести полуокружности радиуса 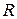 с центром в начале координат, расположенной в верхней полуплоскости.
с центром в начале координат, расположенной в верхней полуплоскости.
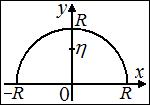 В силу симметрии абсцисса центра тяжести
В силу симметрии абсцисса центра тяжести 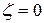 . Найдем ординату центра тяжести, используя первую теорему Паппа-Гульдина. Поверхность, образованная при вращении кривой вокруг оси
. Найдем ординату центра тяжести, используя первую теорему Паппа-Гульдина. Поверхность, образованная при вращении кривой вокруг оси  , является сферой, ее площадь
, является сферой, ее площадь 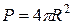 . Длина кривой равна половине длины окружности
. Длина кривой равна половине длины окружности 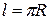 . Подставив эти значения в формулу
. Подставив эти значения в формулу 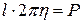 , найдем ординату центра тяжести
, найдем ординату центра тяжести 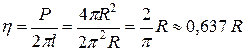 .
.
Пример 2. Найти площадь поверхности вращения полуокружности вокруг касательной, параллельной её диаметру.
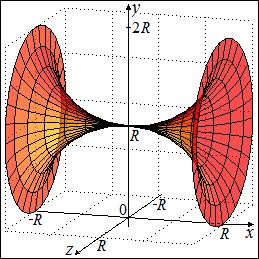 Используем результат, полученный в предыдущем примере. Ордината центра тяжести полуокружности
Используем результат, полученный в предыдущем примере. Ордината центра тяжести полуокружности 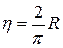 .
.
Тогда радиус окружности, описываемой центром тяжести при вращении полуокружности вокруг касательной, равен 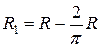 . Из первой теоремы Паппа-Гульдина имеем формулу
. Из первой теоремы Паппа-Гульдина имеем формулу 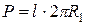 . Отсюда искомая площадь поверхности
. Отсюда искомая площадь поверхности
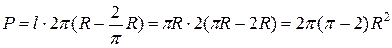 .
.
Вторая теорема Паппа-Гульдина. Объём тела, образованного вращением плоской фигуры вокруг не пересекающей её оси, равен произведению площади фигуры на путь, проходимый центром тяжести этой фигуры. В случае вращения вокруг оси  теорема записывается формулой
теорема записывается формулой
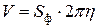 .
.
Доказательство. Рассмотрим случай плоской кривой, когда она задана явно уравнением 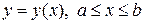 . Фигура под графиком этой кривой является криволинейной трапецией. Ордината центра тяжести плоской фигуры находится по формуле
. Фигура под графиком этой кривой является криволинейной трапецией. Ордината центра тяжести плоской фигуры находится по формуле 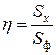 . Применяя формулу для вычисления статического момента
. Применяя формулу для вычисления статического момента 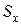 , получаем
, получаем 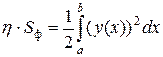 . Домножим на число
. Домножим на число 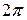 обе части этого равенства:
обе части этого равенства:
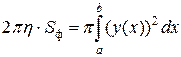 .
.
В правой части стоит объем тела, полученного вращением кривой вокруг оси  . Левая часть является произведением площади фигуры на длину окружности, описываемой центром тяжести этой фигуры.
. Левая часть является произведением площади фигуры на длину окружности, описываемой центром тяжести этой фигуры.
|
|
|
Теорема доказана.
Пример 3. Найти координаты центра тяжести полукруга радиуса R с центром в начале координат, расположенного в верхней полуплоскости.
Воспользуемся второй теоремой Паппа-Гульдина. При вращении вокруг оси  полукруг образует шар. Объем шара равен
полукруг образует шар. Объем шара равен 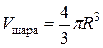 , площадь полукруга равна
, площадь полукруга равна  . Подставляя эти значения в формулу
. Подставляя эти значения в формулу 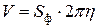 , находим
, находим 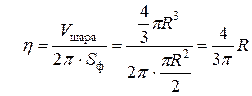 .
.
 2015-05-05
2015-05-05 5180
5180







