Это преобразование можно получить из преобразования Лапласа или Фурье для дискретного сигнала xg(t)
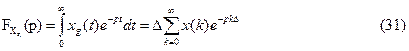 |
Определим одностороннее преобразование Лапласа (для сигналов, определенных при t ³0 для дискретного сигнала вида (1)):
При p=j w из (31) следует преобразование Фурье для дискретного сигнала.
 |
Если обозначить:
 |
то преобразование Лапласа (31) переходит в Z- преобразование дискретного сигнала Xg(t):
 |
Очевидно, что из преобразования Фурье дискретного сигнала Xg(t) при
следует также Z-преобразование X(z).
Справедливо и обратное утверждение: из Z-преобразования X(z) дискретного сигнала (33) при 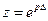 следует его преобразование Лапласа. (Или из X(z) при
следует его преобразование Лапласа. (Или из X(z) при 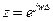 следует преобразование Фурье сигнала).
следует преобразование Фурье сигнала).
 |
Если дискретный сигнал Xg(t) определен и при t<0, то вместо (33) можно ввести более общее преобразование для такого сигнала:
Следует оговорить сходимость X(z) при неограниченном числе слагаемых в (33) или (35). Отсчеты x(k) всегда удовлетворяют условию |x(k)|<CRk, k > 0, C>0 и R>0 постоянные вещественные числа. Тогда (33) сходится при всех Z, для которых │z│>R (т.е. в кольцевой области с радиусом сходимости R). В области сходимости X(z) представляет собой аналитическую функцию переменной z, не имеющую в этой области ни полюсов, ни существенно особых точек.
|
|
|
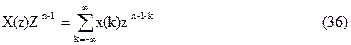 |
Для нахождения x(k) по X(z) (т.е. обратного Z-преобразования) умножим левую и правую части (33) на Zn-1
 |
Возьмем от левой и правой частей (36) интеграл по z по замкнутому контуру в области аналитичности, охватывающей все полюсы функции X(z)zn-1. Получим следующий результат:
Этот результат следует из теоремы Коши при интегрировании функции комплексного переменного z:
 |
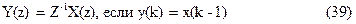 |
Наиболее важное свойство Z-преобразования связано со сдвигом сигнала во времени:
Таким образом, Z-преобразование дискретного сигнала y(t), у которого все отсчеты смещены на один такт (в сторону запаздывания) относительно дискретного сигнала Xg(t), равно произведению z-1 на X(z). Можно сказать, что z-1 является оператором сдвига на один такт в сторону запаздывания. Для доказательства (39) запишем Z-преобразование последовательности{y(k)=x(k-1)}:
 |
Вводя переменную k-1=n, из (40) получим (39). Очевидно, если
y(k)=x(k-n), то Y(z)=z-1X(z).
Рассмотрим дискретную свертку конечной протяженности 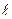 :
:
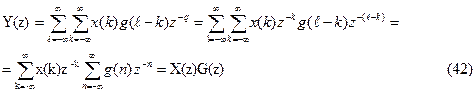 |
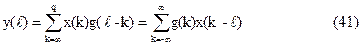 |
Найдем Z-преобразование этой свертки:
Таким образом, свертка двух дискретных сигналов соответствует произведению их Z-преобразований.
Покажем, что импульсная характеристика ЦФ {g(0), g(1)…g(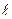 )} является его откликом на единичный импульс (1,0,0,0,0,…). Действительно, при воздействии единичного импульса формула (41) принимает вид:
)} является его откликом на единичный импульс (1,0,0,0,0,…). Действительно, при воздействии единичного импульса формула (41) принимает вид:
|
|
|
y(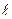 )=g(
)=g(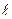 ),
), 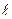 =0,1,2… (43)
=0,1,2… (43)
Если импульсная характеристика ЦФ финитна, то
y(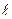 )=0 при
)=0 при 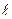 =Q+1, (44)
=Q+1, (44)
где (L+1)- число тактовых отрезков на интервале финитности.
Рассмотрим прохождение через линейный ЦФ гармонической последовательности вида x(t)=ej(wt+ j) или в дискретном виде:
x(k)=ej (wkD + j) (45)
Согласно формуле свертки (41) с учетом (45) находим выходной сигнал:
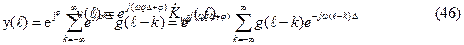 |
Введем над знаком суммы новый индекс суммирования q-k=n и учтем, что из соображений реализуемости g(n)=0 при n<0. Тогда:
 |
где
 |
- комплексная передаточная характеристика ЦФ. Импульсная характеристика ЦФ в реальном масштабе времени будет иметь вид:
причем Ќцф(f) является преобразованием Фурье от дискретного сигнала вида (48).
Как следует из (47), Ќцф(f) является периодической функцией частоты дискретизации Fg=1/Δ (как и спектр дискретного сигнала).
Если в (47) ввести переменную z=ejwD, то получим Z-преобразование импульсной характеристики ЦФ:
 |
H(z) называют системной функцией стационарного линейного ЦФ.
 |
Из (42) при замене G(z) на H(z) видно, что системная функция ЦФ определяется как отношение Z-преобразования выходного сигнала фильтра к Z-преобразованию входного сигнала:
 |
Если в системной функции ЦФ положить
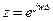 , получим частотную характеристику ЦФ
, получим частотную характеристику ЦФ
Таким образом, применение Z-преобразований позволяет проводить анализ цифровых фильтров теми же методами, что и анализ аналоговых линейных цепей.
 2015-05-06
2015-05-06 918
918








