Затухающие колебания

в реальных условиях материальная точка, совершающая колебания, испытывает сопротивление движению, поэтому кроме восстанавливающей силы на нее действует сила сопротивления среды, направленная в сторону противоположную движению материальной точки (рис. 6).

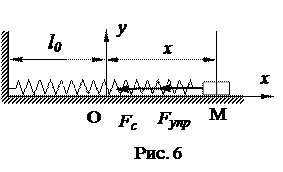
Сопротивление воздуха при малых скоростях движения пропорционально первой степени скорости: 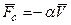. Выбрав начало координат в положении равновесия –т. О, запишем основное уравнение динамики в проекции на ось x: 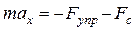или 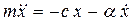. Отсюда получим

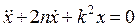(16)

– это уравнение описывает движение точки под действием восстанавливающей силы с учетом сопротивления среды. Здесь обозначено 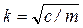, 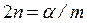. Найдем корни характеристического уравнения 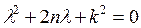, соответствующего уравнению (16):

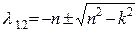. (17)

Если 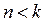(случай малого сопротивления среды), то корни характеристического уравнения 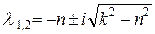являются комплексно-сопряженными, и решение уравнения (16) имеет вид:

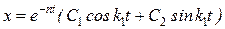. (18)

В решении (18) обозначено: .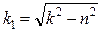

Взяв производную по времени от (18), и использовав начальные условия, можно определить постоянные интегрирования С ₁ и С ₂.

Решение (18) можно записать в виде: 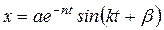. (19)

График функции (19) показан на рис. 7.

Из графика видно, что движение точки в этом случае носит колебательный характер. При этом максимальные отклонения точки от положения равновесия с течением времени убывают по экспоненте. Такие колебания называются затухающими. Функция (19) не является периодической, тем не менее, периодом колебаний в этом случае называют промежуток времени между двумя последовательными максимальными отклонениями точки от положения равновесия в одну сторону. Его можно найти по формуле

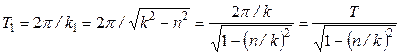, (20)

где T – период соответствующих свободных колебаний. Из формулы (20) видно, что 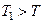. Скорость убывания амплитуды колебаний характеризует коэффициент, называемый декрементом колебаний: 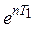. Этот коэффициент показывает, во сколько раз уменьшается максимальное отклонение точки от положения равновесия за один период.

13. Случай апериодического движения (n > k)

Если 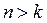(случай большого сопротивления среды), то корни характеристического уравнения (17) 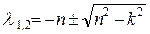являются действительными и отрицательными. решение уравнения (16) в этом случае имеет вид:

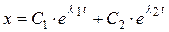. (21)

Взяв производную по времени от (21) и использовав начальные условия, можно определить постоянные интегрирования С ₁ и С ₂.

Сценарии развития событий в этом случае показаны на рис. 8.

Из графиков видно, что движение точки в этом случае носит не колебательный характер и точка с течением времени асимптотически приближается к положению равновесия: _.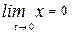

При этом кривая – 1 соответствует случаю, когда 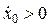; кривая 2 соответствует случаю, когда 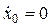; кривая 3 соответствует случаю, когда 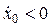. Во всех трех примерах принято, что x ₀ > 0.

14. Случай апериодического движения (n = k)

Если 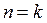(это также случай большого сопротивления среды), то корень характеристического уравнения (17) 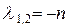, то есть является кратным, действительным и отрицательным. решение уравнения (16) в этом случае имеет вид:

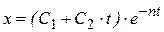. (22)

Взяв производную по времени от (22) и использовав начальные условия, можно определить постоянные интегрирования С ₁ и С ₂. В этом случае, найдя предел по правилу Лопиталя, получим

.

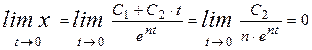Следовательно, и в этом случае движение точки носит неколебательный характер, и точка с течением времени асимптотически приближается к положению равновесия. Сценарии развития событий в этом случае такие же, как и на рис. 8.