Формула Коши

Теорема 7.12 Пусть:

1) f (x) и g (x) определены и непрерывны на сегменте [ a, b ],

2) f (x) и g (x) дифференцируемы в интервале (a, b),

3) g ’(x) ¹ 0 " x Î (a, b).

Тогда: $ точка c Î (a, b): 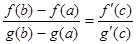. (1)

(это формула Коши)

Доказательство.

Прежде всего отметим, что знаменатель в левой части формулы (1) не равен нулю, то есть g (a) ¹ g (b). В самом деле, если допустить, что g (a) = g (b), то функция g (x) будет удовлетворять всем условиям теоремы Ролля, и тогда найдется такая точка на интервале (a, b), в которой g ’(x) = 0, что противоречит условию 3) нашей теоремы.

1-й способ (неверный).

f (b) – f (a) = f ’(c)(b – a),

g (b) – g (a) = g ’(c)(b – a).

Разделив эти равенства друг на друга, получим формулу (1). Это доказательство не годится, так как точки c, вообще говоря, разные.

2-й способ.

Введем функцию F (x) = f (x) – f (a) - 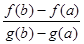(g (x) – g (a)).

F (x) удовлетворяет всем условиям теоремы Ролля. В частности, F (a) = F (b) = 0.

По теореме Ролля, $ точка c Î (a, b): F ’(c) = 0.

f ’(c) - 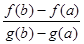g ’(c) = 0. .

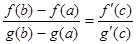Теорема доказана.

Формула Лагранжа является частным случаем формулы Коши в случае, когда g (x) = x. В этом случае g ’(c) = 1, g (a) = a, g (b)= b.