2015-04-20
388
1. Определяем среднее арифметическое первого ряда:
N
| `x 1 = | ∑хi i=1 | = | 115+120+120+125+120+130+125+120+115+120 | = 121 |
| N |
2. Определяем среднее арифметическое второго ряда:
N
| `x 2 = | ∑хi i=1 | = | 150+145+155+140+140+145+150+160+150+150 | = 148,5 |
| N |
3. Рассчитываем среднее квадратическое отклонение в первом ряду (при N < 30):
| S1 = | √ | N ∑ di2 i=1 | = | √ | ∑(`x i - `x 1)2 i=1 | = | √ | = 4,6 | |
| N -1 |
4. Рассчитываем среднее квадратическое отклонение в втором ряду
(при N < 30):
| S2 = | √ | N ∑ di2 i=1 | = | √ | ∑(xi -`x 2)2 i=1 | = | √ | = 6,3 | |
| N - 1 |
5. Определяем стандартную ошибку среднего арифметического для первого ряда:
| µ`x 1 = | S1 | = | 4,6 | = 1,5 |
| 
|
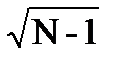
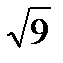
6. Определяем стандартную ошибку среднего арифметического для второго ряда:
| µ`x 2 = | S2 | = | 6,3 | = 2,1 |
|
| 
|
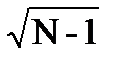
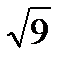
7. Находим достоверность различия между средними величинами:
| Т = | ``x 1 - `x 2 | = | 148,5 - 121 | = | 27,5 | = 10,7 |
| √µ2 `x 1+ µ2 `x 2 | √ (2,1)2 + (1,5)2 | 2,58 |
Поскольку при N = 10 (N – 1 = 9) наблюдениях показатель T превысил указанный в таблице значений коэффициента Стьюдента (таблица 3.1) уровень достоверности различия более 99,9 %, т.е. средние двух групп статистически значимо различаются с доверительной вероятностью 99,9 %.
